На этом шаге мы рассмотрим основные свойства операции примитивной рекурсии.

Операция примитивной рекурсии, так же как и операция подстановки, сохраняет свойство всюду определенности и алгоритмической вычислимости.

Свойство 1.

Сохранение свойства всюду определенности функций, т.е. если g(x₁, ..., x_n) и h(x₁, ..., x_n, y, z) всюду определенные функции, то f(x₁, ..., x_n, y) тоже будет всюду определенная функция, где f = R(g, h).

Доказательство.

Берем произвольный набор (x₁, ..., x_n, y) и докажем, что на этом наборе функция f определена. Доказательство проводим методом математической индукции по y.

1 шаг. Пусть y=0. Тогда по определению операции примитивной рекурсии получаем, что f(x₁, ..., x_n, 0) = g(x₁, ..., x_n). Так как функция g всюду определенная функция по условию, то функция f определена на наборе (x₁, ..., x_n, 0).
2 шаг. Предположим, что функция f определена на наборе (x₁, ..., x_n, y).
3 шаг. Докажем, что функция f определена на наборе (x₁, ..., x_n, y+1). По определению операции примитивной рекурсии получаем, что f(x₁, ..., x_n, y+1) = h(x₁, ..., x_n, y, f(x₁, ..., x_n, y)).

А функция h обладает свойством всюду определенности по условию. Следовательно, функция f определена на наборе (x₁, ..., x_n, y+1). Так как функция f является арифметической функцией, то метод математической индукции позволяет сделать вывод, что она всюду определена.

Свойство 2.

Сохранение алгоритмической вычислимости функций, т.е., если g(x₁, ..., x_n) и h(x₁, ..., x_n, y, z) являются алгоритмически вычислимыми функциями, то существует алгоритм A_f, вычисляющий функцию f(x₁, ..., x_n, y), где f(x₁, ..., x_n, y) = R(g(x₁, ..., x_n), h(x₁, ..., x_n, y, z)).

Доказательство.

Пусть задан произвольный набор (x₁, ..., x_n, y). Докажем, что функция f алгоритмически вычислима на этом наборе. Для доказательства поступим следующим образом. Сначала применяем алгоритм A_g, вычисляющие функцию g(x₁, ..., x_n) на набору (x₁, ..., x_n). В случае остановки через конечное число шагов получаем значение функции g(x₁, ..., x_n) на этом наборе, равное по определению операции примитивной рекурсии: g(x₁, ..., x_n) = f(x₁, ..., x_n, 0).

После этого используем алгоритм A_h, который вычисляет значение функции h(x₁, ..., x_n, y, z). Этот алгоритм последовательно применяем к следующим наборам:

. . . .

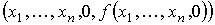
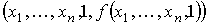
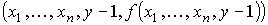
Если каждый раз работа алгоритма A_h завершается результативно, то мы получаем соответствующие значения функции h(x₁, ..., x_n, y, z), равные значениям функции f(x₁, ..., x_n, y) (это следует из определения операции примитивной рекурсии):

. . . .

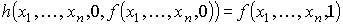
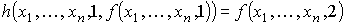
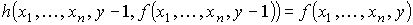
А если не произошло остановки алгоритма A_g в наборе (x₁, ..., x_n) или не закончился результативно алгоритм A_h на одном из этапов вычисления значения функции h(x₁, ..., x_n, y, z), (т.е. например, при вычислении h(x₁, ..., x_n, y', f(x₁, ..., x_n, y')) , где y' принадлежит {0, 1, 2, ..., y-1}), то переход к следующему этапу никогда не произойдет и искомый алгоритм считается не применимым к набору (x₁, ..., x_n, y).

Приведем несколько примеров получения вычислимых функций с помощью операции примитивной рекурсии.

Пример 1. Пусть задано

и покажем, что f(x,y) = R(g(x), h(x,y,z)), где f(x,y) = x + y.

Согласно определению операции примитивной рекурсии:

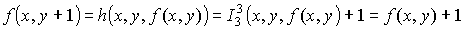
Тогда:

. . . . .

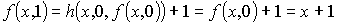
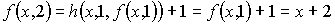
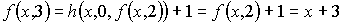
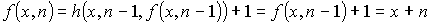
Предположим, что для некоторого n, принадлежащего N, последнее равенство справедливо и докажем, что тогда

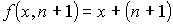
Действительно, пусть f(x,n) = x + n для некоторого n, принадлежащего N. Тогда по определению операции примитивной рекурсии получаем, что:

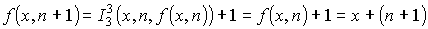
Таким образом, функция f(x,y) = x + y получается из функции и с помощью операции примитивной рекурсии.

Пример 2. Пусть

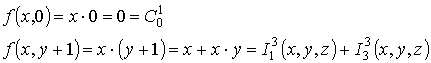
Для решения задачи нахождения элементарных функций воспользуемся определением операции примитивной рекурсии, после чего получим, что

Тогда:

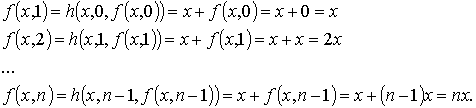
Очевидно, функция – есть результат операции примитивной рекурсии над функциями и .

Определение. Примитивно рекурсивным описанием функции (ПРО) f называется конечная последовательность функций , удовлетворяющая следующим условиям:

последний член этой последовательности есть сама функция f, т.е. ;
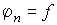для любого i=1, 2, ..., n 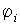- есть либо элементарная функция, либо получается из предшествующих ей функций в этой последовательности с помощью одной из операции примитивной рекурсии или подстановки.

Определение. Функция f называется примитивно рекурсивной функцией (ПРФ), если существует хотя бы одно ее ПРО.

Из определения следует, что всякая примитивно рекурсивная функция f имеет несколько различных ПРО.

Например, для функции g(x,y) = x + y ПРО является последовательность следующих функций:

На следующем шаге мы рассмотрим основные свойства ПРФ.

Предыдущий шаг Содержание Следующий шаг