На этом шаге мы рассмотрим операцию навешивания ограниченного квантора над предикатами.
Пусть задан двуместный предикат p(x,y), где в общем случае x = (x1, ..., xn).
Определение. Говорят, что предикат R(x,z) получен из предиката p(x,y) с применением операции навешивания ограниченного квантора существования, т.е. R(x,z) = (∃y)y<=zp(x,y), если выполняется следующее равенство:
R(x,z) = p(x,0) V p(x,1) V ... V p(x,z) (27)
Определение. Говорят, что предикат Q(x,z) получен из предиката p(x,y) с применением операции навешивания ограниченного квантора всеобщности, т.е. Q(x,z) = (∀y)y<=zp(x,y), если выполняется следующее равенство:
Q(x,z) = p(x,0) ∧ p(x,1) ∧ ... ∧ p(x,z) (28)
Приведем пример. Пусть p(x,y) = (x+y=5). Рассмотрим R(x,z) = (∃y)y<=zp(x,y) и Q(x,z) = (∀y)y<=zp(x,y). Очевидно:
R(4,2) = (∃y)y<=2p(4+y=5) = и
R(1,3) = (∃y)y<=3p(1+y=5) = л
Q(4,2) = (∀y)y<=2p(4+y=5) = л
Q(5,0) = (∀y)y<=0p(5+y=5) = и
- Теорема 3.
- Операция навешивания ограниченных кванторов существования и всеобщности сохраняет свойство примитивной рекурсивности функций относительно совокупности {p}.
- Доказательство.
- Пусть задан предикат p(x,y) и φ(x,y) - представляющая его функция и пусть
R(x,z) = (∃y)y<=zp(x,y).
Представляющую функцию предиката R(x, z) обозначим через φR(x,z) и покажем, что ее можно представить следующим образом:
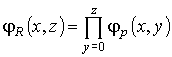. (29)
Действительно:
- Пусть предикат R(x,z0) = и. Тогда по определению операции навешивания ограниченного квантора существования, найдется y0
такое, что 0<=y0<=z0 и p(x,y0) = и, следовательно
φ(x,y0) = 0. Отсюда следует, что:
.
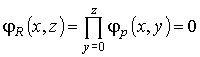- Предположим, что предикат R(x,z0) = л. Тогда по определению операции навешивания ограниченного квантора существования, для любого набора
(x,y) p(x,y) = л, следовательно φ(x,y0) = 1 и
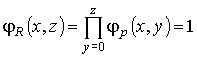
Пусть Q(x,z) = (∀y)y<=zp(x,y). Аналогично доказывается случай, когда задана операция навешивания ограниченного квантора всеобщности. Легко можно доказать, что в качестве представляющей функции предиката можно брать
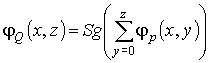(30)
и φR(x,z) является ПРФ относительно совокупности {φp(x,y)} (докажите самостоятельно).
- Пусть предикат R(x,z0) = и. Тогда по определению операции навешивания ограниченного квантора существования, найдется y0
такое, что 0<=y0<=z0 и p(x,y0) = и, следовательно
φ(x,y0) = 0. Отсюда следует, что:
Пусть задана совокупность функций {φ1, ..., φk} и совокупность предикатов {p1, ..., pm}.
Определение. Функция f(x1, ..., xn) называется ПРФ относительно заданной совокупности функций и предикатов, если она ПРФ относительно совокупности Ψ = {φ1, ..., φm, φp1, ..., φpm}, где φpi - представляющая функция предиката pi, 1<=i<=m.
На следующем шаге мы рассмотрим кусочное задание функции.
