Ниже перечислены пять разновидностей "О-большого" в порядке убывания скорости выполнения:
- O(log n), или логарифмическое время. Пример: бинарный поиск.
- О(n), или линейное время. Пример: простой поиск.
- О(n * log n). Пример: эффективные алгоритмы сортировки (быстрая сортировка).
- О(n2). Пример: медленные алгоритмы сортировки (сортировка выбором).
- О(n!). Пример: очень медленные алгоритмы (задача о коммивояжере).
Рассмотрим задачу. Предположим, вы строите сетку из 16 квадратов.
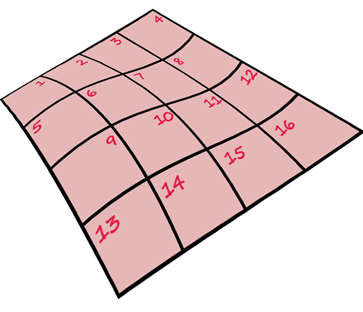
Алгоритм 1. Как вариант можно нарисовать 16 квадратов, по одному за раз. Чтобы нарисовать 16 квадратов, потребуется 16 шагов (рисование квадрата считается одной операцией).
Алгоритм 2. Сложите лист пополам. На этот раз операцией считается сложение листка. Получается, что одна операция создает сразу два прямоугольника. Сложите бумагу еще раз, а потом еще и еще.
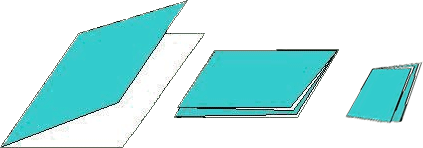
Разверните листок после четырех сложений - получилась сетка. Каждое сложение удваивает количество прямоугольников. За 4 операции можно создать 16 прямоугольников.

Для решения этой задачи вы можете выбрать один из 5 алгоритмов. При использовании первого алгоритма сетка будет построена за время O(log n). В секунду выполняются до 10 операций. С временем O(log n) для построения сетки из 16 квадратов потребуются 4 операции (log 16 равен 4). Итак , сетка будет построена за 0,4 секунды.
А если бы было нужно построить 1024 квадрата? На это бы потребовалось log 1024 = 10 операций, или 1 секунда.
Второй алгоритм работает медленнее: за время О(n). Для построения 16 прямоугольников потребуется 16 операций, а для построения 1024 прямоугольников - 1024 операции. Сколько это составит в секундах?
Ниже на рисунке показано, сколько времени потребуется для построения сетки с остальными алгоритмами:
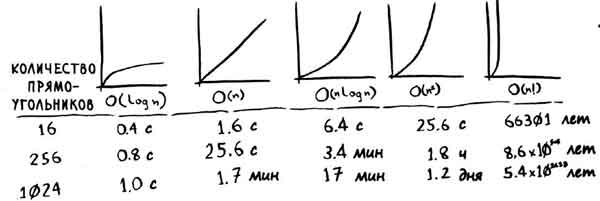
Существуют и другие варианты времени выполнения, но эти пять встречаются чаще всего.
На практике "О-большое" не удается легко преобразовать в количество операций с такой точностью.
Подведем некотрые итоги:
- Скорость алгоритмов измеряется не в секундах, а в темпе роста количества операций.
- По сути формула описывает, насколько быстро возрастает время выполнения алгоритма с увеличением размера входных данных.
- Время выполнения алгоритмов выражается как "О-большое".
- Время выполнения O(log n) быстрее О(n), а с увеличением размера списка, в котором ищется значение, оно становится намного быстрее.
На следующем шаге рассмотрим еще один пример применения бинарного поиска при решении олимпиадной задачи по программированию.
