На этом шаге рассмотрим применение алгоритма бинарного поиска при решении конкретных задач.
Рассмотрим применение алгоритма бинарного поиска при решении следующей задачи (Региональный этап Всероссийской олимпиалы школьников по информатике 2016 г., первый тур).
Задача 2. Космическое поселение
Ограничение по времени: 1 секунда
Ограничение по памяти: 256 мегабайт
Для освоения Марса требуется построить исследовательскую базу. База должна состоять из n одинаковых модулей, каждый из которых представляет собой прямоугольник.
Каждый модуль представляет собой жилой отсек, который имеет форму прямоугольника размером a × b метров. Для повышения надежности модулей инженеры могут добавить вокруг каждого модуля слой дополнительной защиты. Толщина этого слоя должна составлять целое число метров, и все модули должны иметь одинаковую толщину дополнительной защиты. Модуль с защитой, толщина которой равна d метрам, будет иметь форму прямоугольника размером (a + 2d) × (b + 2d) метров.
Все модули должны быть расположены на заранее подготовленном прямоугольном поле размером w × h метров. При этом они должны быть организованы в виде регулярной сетки: их стороны должны быть параллельны сторонам поля, и модули должны быть ориентированы одинаково.
Требуется написать программу, которая по заданным количеству и размеру модулей, а также размеру поля для их размещения, определяет максимальную толщину слоя дополнительной защиты, который можно добавить к каждому модулю.
Для значений n = 11, a = 2, b = 3, w = 21, h = 25, возможный вариант реализации задачи представлена на рис.1.
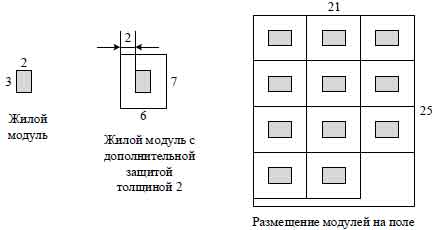
Рис.1. Вариант реализации задачи
Решение:
При решении задачи возможны два варианта размещения модулей: горизонтальный и вертикальный (по условию, модули должны быть ориентированы одинаково). Рассмотрим вариант, при которм сторона длиной a ориентирована вдоль стороны поля длиной w.
Тогда, после установления защиты толщиной d, количество модулей, которые можно разместить вдоль стороны длины w, рассчитаем по формуле:
Аналогично, количество модулей, которые можно установить вдоль другой стороны рассчитаем по формауле:
Тогда, количество модулей, которые можно установить на поле размером w × h метров, получим по формуле:
Если по этой формуле получим, что количество модулей больше или равно n, то защиту толщиной d установить можно, иначе нельзя.
На следующем шаге рассмотрим программную реализацию данного подхода к решению задачи.
