На этом шаге рассмотрим стек вызовов с рекурсией.
Рекурсивные функции тоже используют стек вызовов. Посмотрим, как это делается, на примере функции вычисления факториала. Вызов fact(5) записывается в виде 5! и определяется следующим образом: 5! = 5*4*3*2*1
.По тому же принципу fact(З) соответствует 3*2*1. Рекурсивная функция для вычисления факториала числа выглядит так:
int fact(int x) { if (x==1) return 1; else return x*factorial(x-1); }
В программу включается вызов fact(З). Проанализируем этот вызов строку за строкой и посмотрим, как изменяется стек вызовов. Стоит напомнить, что верхний блок в стеке сообщает, какой вызов fact является текущим.
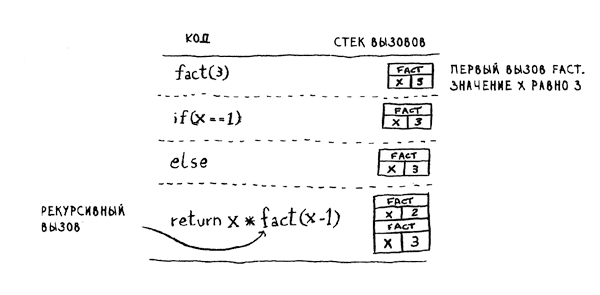
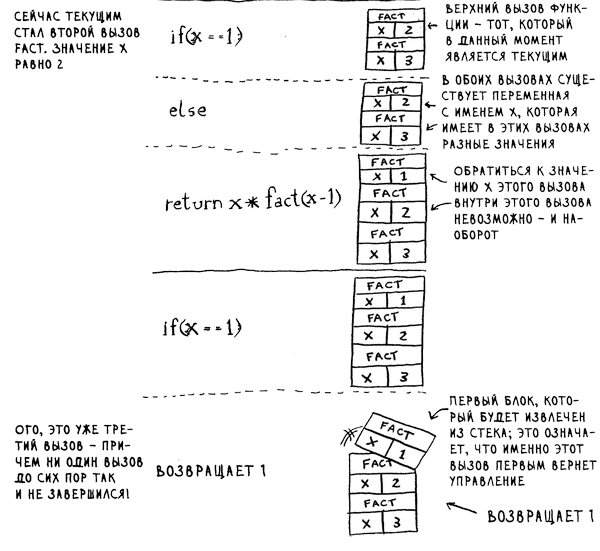
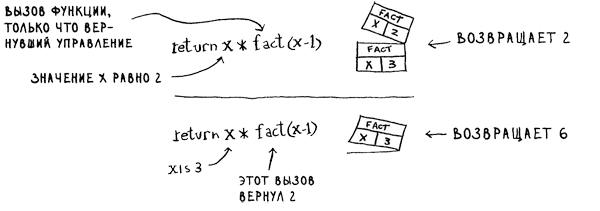
Здесь важно, что каждый вызов создает собственную копию х. Обратиться к переменной х, принадлежащей другой функции, невозможно.
Стек играет важную роль в рекурсии. В начальном примере (шаг 14) были представлены два решения поиска сюрприза. Вспомните, как выглядел первый:
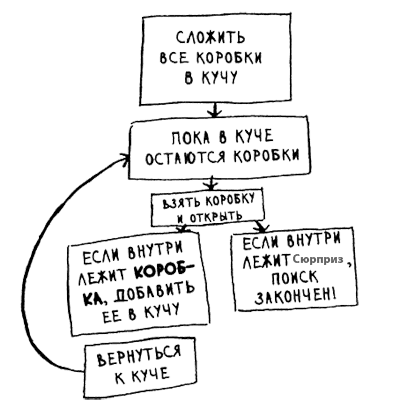
В этом случае все коробки лежат в одном месте и вы всегда знаете, в каких коробках еще нужно искать сюрприз.
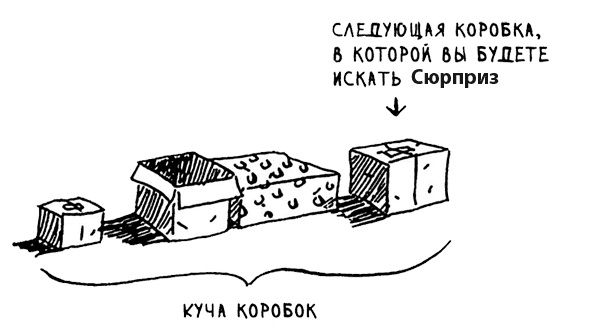
Но в рекурсивном решении никакой кучи не существует.
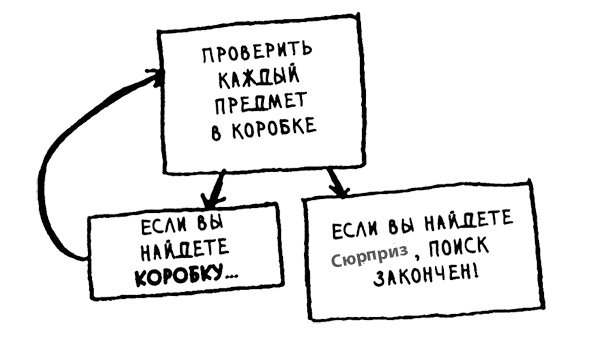
Если кучи нет, то как ваш алгоритм узнает, в каких коробках еще нужно искать? Пример:
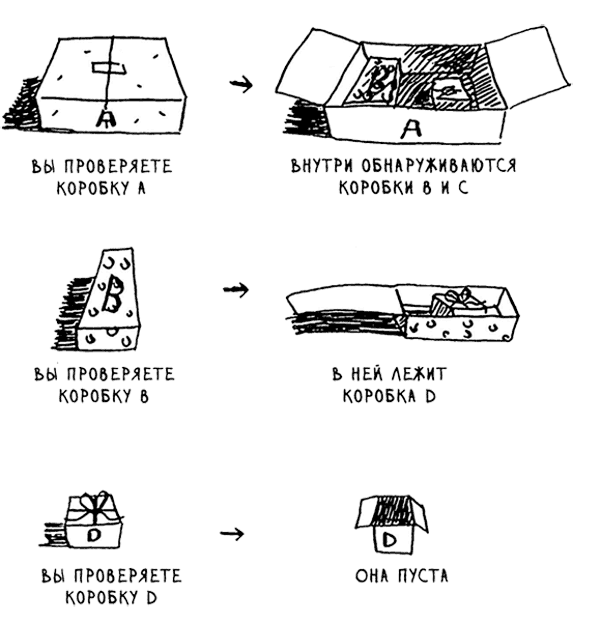
К этому моменту стек вызовов выглядит примерно так:
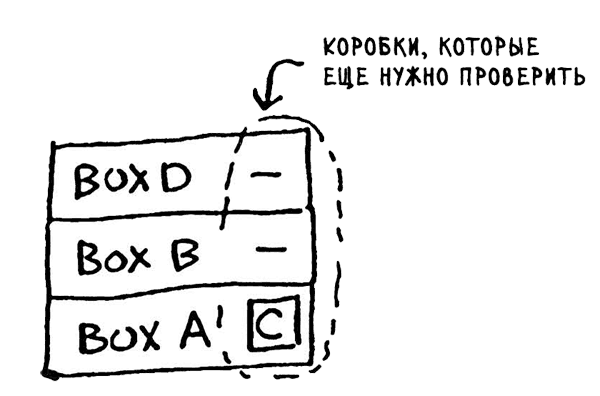
"Куча коробок" хранится в стеке! Это стек незавершенных вызовов функции, каждый из которых ведет собственный незаконченный список коробок для поиска. Стек в данном случае особенно удобен, потому что вам не нужно отслеживать коробки самостоятельно - стек делает это за вас.
Стек удобен, но у него есть своя цена: сохранение всей промежуточной информации может привести к значительным затратам памяти. Каждый вызов функции занимает не много памяти, но если стек станет слишком высоким, это будет означать, что ваш компьютер сохраняет информацию по очень многим вызовам. На этой стадии есть два варианта:
- переписать код с использованием цикла.
- иногда можно воспользоваться так называемой хвостовой рекурсией.
Архив с примером на языке С++ можно взять здесь.
Архив с примером на языке Pascal можно взять здесь.
На следующем шаге начнем рассматривать быструю сортировку и познакомимся с принципом "разделяй и властвуй".
