На этом шаге рассмотрим принцип "разделяй и властвуй".
На это шаге мы будем исследовать принцип "разделяй и властвуй", хорошо известный рекурсивный метод решения задач.
Алгоритм не особенно полезен, если он способен решать задачу только одного типа, - "разделяй и властвуй" помогает выработать новый подход к решению задач. Это всего лишь еще один инструмент в вашем арсенале.
Начнем с примера. Представьте, что вы фермер, владеющий земельным участком. Вы хотите равномерно разделить землю на одинаковые квадратные участки. Участки должны быть настолько большими, насколько это возможно.
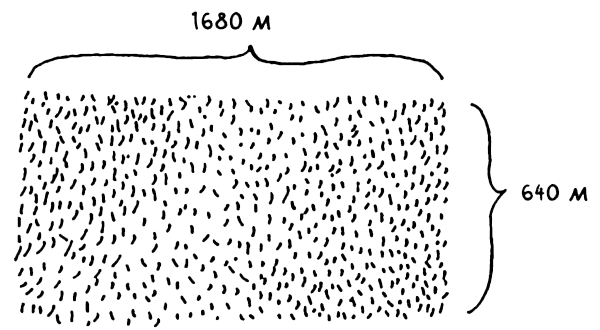
Так что ни одно из следующих решений не подойдет.
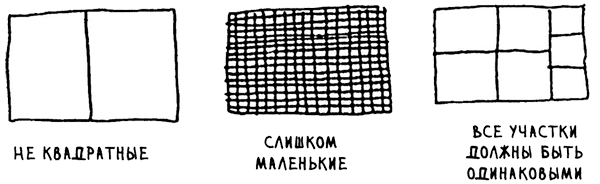
Как определить наибольший размер квадрата для участка? Воспользуемся стратегией "разделяй и властвуй"! Алгоритмы на базе этой стратегии являются рекурсивными.
Решение задачи методом &uot;разделяй и властвуй" состоит из двух шагов:
- Сначала определяется базовый случай. Это должен быть простейший случай из всех возможных.
- Задача делится или сокращается до тех пор, пока не будет сведена к базовому случаю.
А теперь воспользуемся стратегией "разделяй и властвуй" для поиска решения этой задачи. Каков самый большой размер квадрата, который может использоваться?
Для начала нужно определить базовый случай. Самая простая ситуация - если длина одной стороны кратна длине другой стороны. Предположим, длина одной стороны составляет 25 м, а длина другой 50 м. В этом случае размер самого большого участка составляет 25 м х 25 м, и надел после деления будет состоять из двух участков.
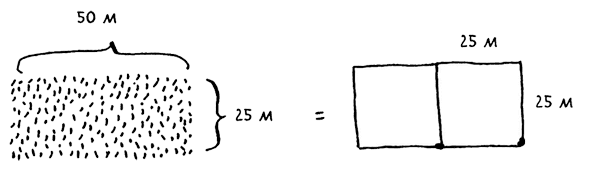
Теперь нужно вычислить рекурсивный случай. Здесь-то вам на помощь и приходит стратегия "разделяй и властвуй". В соответствии с ней при каждом рекурсивном вызове задача должна сокращаться. Как сократить эту задачу? Для начала разметим самые большие участки, которые можно использовать.
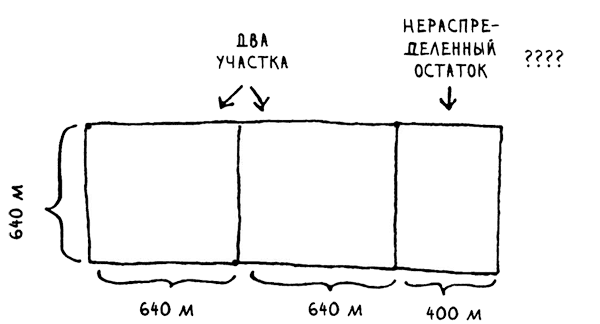
В исходном наделе можно разместить два участка 640 х 640, и еще останется место. Тут-то и наступает момент истины . Нераспределенный остаток - это тоже надел земли, который нужно разделить. Так почему бы не применить к нему тот же алгоритм?
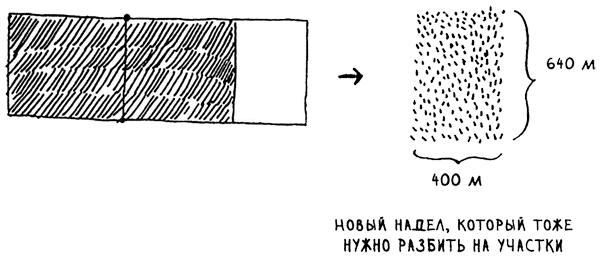
Итак, мы начали с надела 1680 х 640, который необходимо разделить на участки. Но теперь разделить нужно меньший сегмент - 640 х 400. Если вы найдете самый большой участок, подходящий для этого размера, это будет самый большой участок, подходящий для всей фермы. Мы только что сократили задачу с размера 1680 х 640 до 640 х 400!
Применим тот же алгоритм снова. Если начать с участка 640 х 400, то размеры самого большого квадрата, который можно создать, составляют 400 х 400 м.
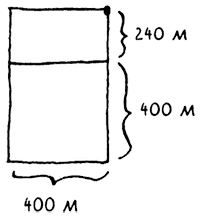
Остается меньший сегмент с размерами 400 х 240 м.
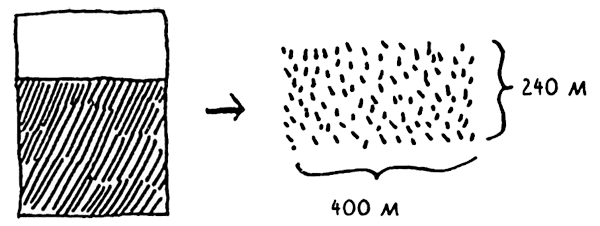
Отсекая поделенную часть, мы приходим к еще меньшему размеру сегмента, 240 x 160 м.
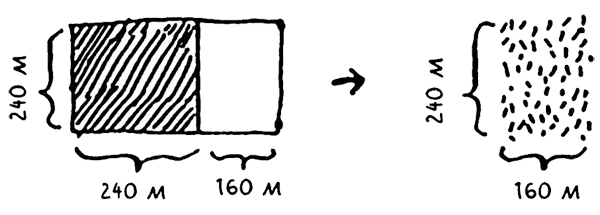
После очередного отсечения получается еще меньший сегмент.
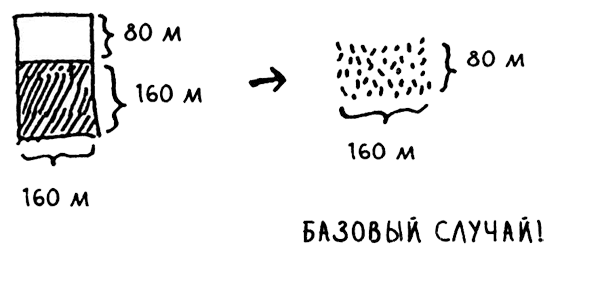
Мы пришли к базовому случаю: 160 кратно 80. Если разбить этот сегмент на квадраты, ничего лишнего не останется! Итак, для исходного надела земли самый большой размер участка будет равен 80 х 80 м.
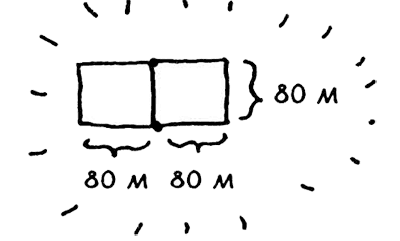
Вспомните, как работает стратегия "разделяй и властвуй":
- Определите простейший случай как базовый.
- Придумайте, как свести задачу к базовому случаю.
"Разделяй и властвуй" - не простой алгоритм, который можно применить для решения задачи. Скорее, это подход к решению задачи.
На следующем шаге рассмотрим еще один пример применения подхода "разделяй и властвуй".
