На этом шаге рассмотрим определение "худшего" и "среднего" случаев выбора опорного элемента быстрой сортировки.
Допустим, у вас имеется простая функция для вывода каждого элемента в списке:
def print_items(list): for item in list: print (item)
Архив с примером на языке Python можно взять здесь.
Эта функция последовательно перебирает все элементы списка и выводит их. Так как функция перебирает весь список, она выполняется за время О(n). Теперь предположим, что вы изменили эту функцию и она делает секундную паузу перед выводом:
from time import sleep def print_items2(list): for item in list: sleep(4) print (item)
Архив с примером на языке Python можно взять здесь.
Перед выводом элемента функция делает паузу продолжительностью в 4 секунды. Предположим, вы выводите список из пяти элементов с использованием обеих функций:


Обе функции проходят по списку один раз, и обе выполняются за время О(n). Как вы думаете, какая из них работает быстрее? Конечно та, которая не делает паузу перед выводом каждого элемента. Следовательно, даже при том, что обе функции имеют одинаковую скорость "О-большое", реально первая функция работает быстрее. Когда вы используете "О-большое", в действительности это означает следующее:
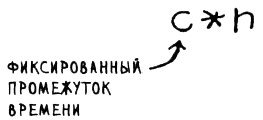
Здесь с - некоторый фиксированный промежуток времени для вашего алгоритма. Он называется константой. Например, время выполнения может составлять 10 миллисекунд * n для print_items против 1 секунды * n для print_i tems2.
Обычно константа игнорируется, потому что если два алгоритма имеют разное время "О-большое", она роли не играет. Для примера возьмем бинарный и простой поиск. Допустим, такие константы присутствуют в обоих алгоритмах.
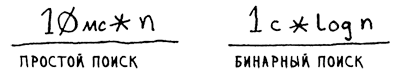
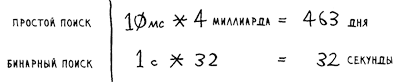
Как видите, бинарный поиск все равно работает намного быстрее. Константа ни на что не повлияла.
Однако в некоторых случаях константа может иметь значение. Один из примеров такого рода - быстрая сортировка и сортировка слиянием. У быстрой сортировки константа меньше, чем у сортировки слиянием, поэтому, несмотря на то, что оба алгоритма характеризуются временем О(n log n), быстрая сортировка работает быстрее. А на практике быстрая сортировка работает быстрее, потому что средний случай встречается намного чаще худшего.
Определим как выглядит средний случай по сравнению с худшим?
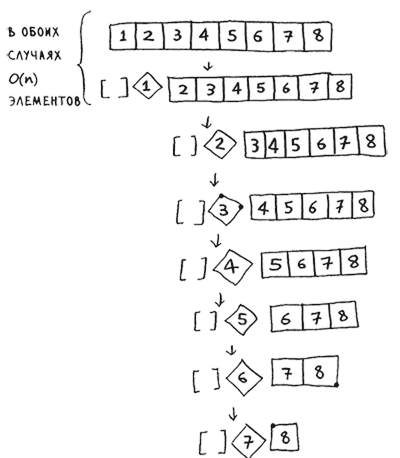
Быстродействие быстрой сортировки сильно зависит от выбора опорного элемента. Предположим, опорным всегда выбирается первый элемент, а быстрая сортировка применяется к уже отсортированному массиву. Быстрая сортировка не проверяет, отсортирован входной массив или нет, и все равно пытается его отсортировать.
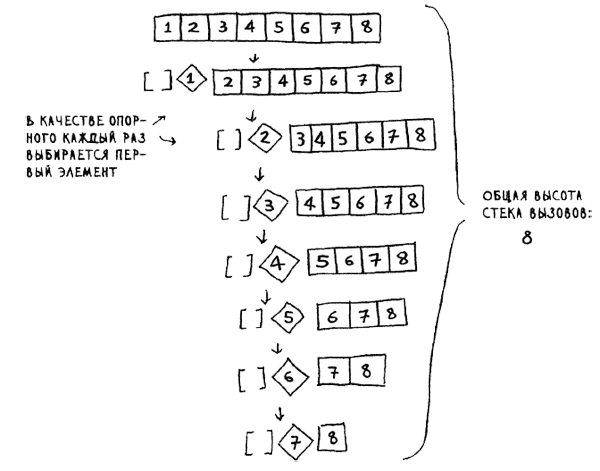
Обратите внимание: на этот раз массив не разделяется на две половины. Вместо этого один из двух подмассивов всегда пуст, так что стек вызовов получается очень длинным. Теперь предположим, что в качестве опорного всегда выбирается средний элемент. Посмотрим, как выглядит стек вызовов в этом случае.
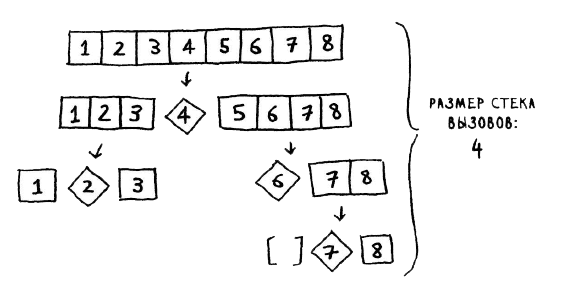
Массив каждый раз делится надвое, поэтому такое количество рекурсивных вызовов излишне. Вы быстрее добираетесь до базового случая, и стек вызовов получается более коротким.
Первый из рассмотренных примеров описывает худший сценарий, а второй - лучший. В худшем случае размер стека описывается как О(n). В лучшем случае он составит O(log n).
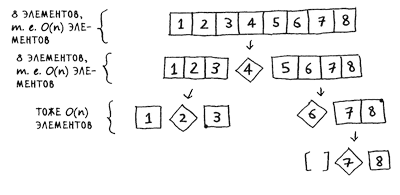
Теперь рассмотрим первый уровень стека. Один элемент выбирается опорным, а остальные элементы делятся на подмассивы. Вы перебираете все восемь элементов массива, поэтому первая операция выполняется за время О(n). На этом уровне стека вызовов вы обратились ко всем восьми элементам. Но на самом деле вы обращаетесь к О(n) элементам на каждом уровне стека вызовов.
Даже если массив будет разделен другим способом, вы все равно каждый раз обращаетесь к О(n) элементам.
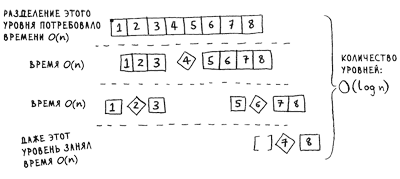
Итак, завершение каждого уровня требует времени О(n).
На следующем шаге рассмотрим хеш-таблицы.
