На этом шаге познакомимся с графами.
Поиск в ширину позволяет найти кратчайшее расстояние между двумя объектами. Однако сам термин "кратчайшее расстояние" может иметь много разных значений. Например, с помощью поиска в ширину можно:
- написать программу для игры в шашки, которая вычисляет кратчайший
- реализовать проверку правописания (минимальное количество изменений, преобразующих ошибочно написанное слово в правильное, например АЛГОРИФМ ->АЛГОРИТМ - одно изменение);
- найти ближайшего к вам врача.
Одни из самых полезных алгоритмов, работают с графами. Предположим, вы находитесь в пункте А и хотите добраться в пункт В. Вы намереваетесь доехать на автобусе с минимальным количеством пересадок. Возможные варианты:
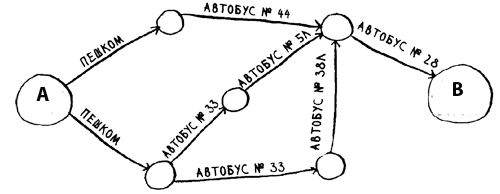
Какой алгоритм использовать для поиска пути с наименьшим количеством шагов?
Можно ли сделать это за один шаг? На следующем рисунке выделены все места, в которые можно добраться за один шаг.
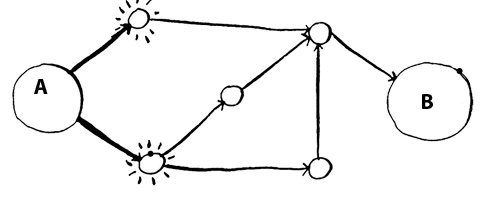
До пункта В невозможно добраться за один шаг.
А можно ли добраться до него за два шага?
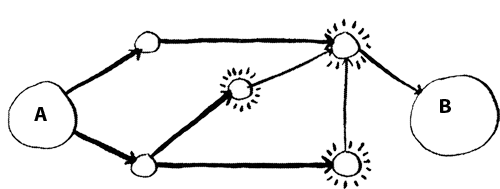
И снова пункт В не выделен, а значит, до него невозможно добраться за два шага. Как насчет трех шагов?
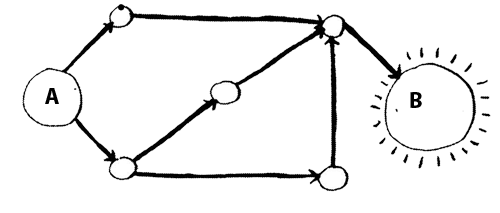
На этот раз пункт В выделен. Следовательно, чтобы добраться из пункта А в пункт В по этому маршруту, необходимо сделать три шага.
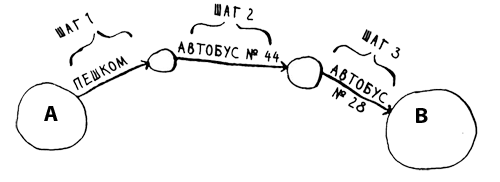
Есть и другие маршруты, которые приведут вас в пункт В, но они длиннее (четыре шага). Алгоритм обнаружил, что кратчайший путь в пункт В состоит из трех шагов. Задача такого типа называется задачей поиска кратчайшего пути. Алгоритм для решения задачи поиска кратчайшего пути называется поиском в ширину.
Чтобы найти кратчайший путь из A в В, нам пришлось выполнить два шага:
- Смоделировать задачу в виде графа.
- Решить задачу методом поиска в ширину.
На следующем шаге продолжим знакомство с графами.
