На этом шаге рассмотрим поиск кратчайшего пути в графе.
Напомним два вопроса, на которые может ответить алгоритм поиска в ширину:
- тип 1: существует ли путь от узла А к узлу В? (Есть ли продавец канцтоваров в вашей сети?)
- тип 2: как выглядит кратчайший путь от узла А к узлу В? (Кто из продавцов находится ближе всего к вам?)
Вы уже знаете, как ответить на вопрос 1; теперь попробуем ответить на вопрос 2. Удастся ли вам найти ближайшего продавца канцелярских товаров? Будем считать, что ваши друзья - это связи первого уровня, а друзья друзей - связи второго уровня.
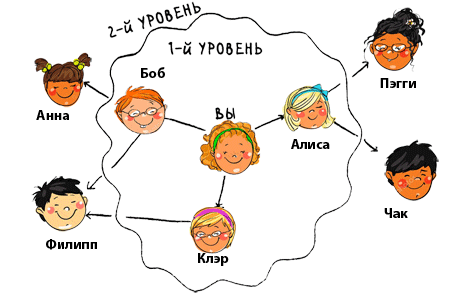
Связи первого уровня предпочтительнее связей второго уровня, связи второго уровня предпочтительнее связей третьего уровня и т. д. Отсюда следует, что поиск по контактам второго уровня не должен производиться, пока вы не будете полностью уверены в том, что среди связей первого уровня нет ни одного продавца канцтоваров. Но ведь поиск в ширину именно это и делает! Поиск в ширину распространяется от начальной точки. А это означает, что связи первого уровня будут проверены до связей второго уровня. Контрольный вопрос: кто будет проверен первым, Клэр или Анна? Ответ: Клэр является связью первого уровня, а Анна - связью второго уровня. Следовательно, Клэр будет проверена первой. Также можно объяснить это иначе: связи первого уровня добавляются в список поиска раньше связей второго уровня.
Вы двигаетесь вниз по списку и проверяете каждого человека (является ли он продавцом канцтоваров). Связи первого уровня будут проверены до связей второго уровня, так что вы найдете продавца канцтоваров, ближайшего к вам. Поиск в ширину находит не только путь из А в В, но и кратчайший путь.
Обратите внимание: это условие выполняется только в том случае, если поиск осуществляется в порядке добавления людей. Другими словами, если Клэр была добавлена в список до Аннны, то проверка Клэр должна быть выполнена до проверки Анны. А что произойдет, если вы проверите Анну раньше, чем Клэр, и обе они окажутся продавцами канцтоваров? Анна является связью второго уровня, а Клэр - связью первого уровня. В результате будет найден продавец канцтоваров, не ближайший к вам в сети. Следовательно, проверять связи нужно в порядке их добавления. Для операций такого рода существует специальная структура данных, которая называется очередью.
На следующем шаге рассмотрим структуру данных "очередь".
