На этом шаге познакомимся с алгоритмом Дейкстры.
В шаге 35 мы узнали, как найти путь из точки А в точку В.
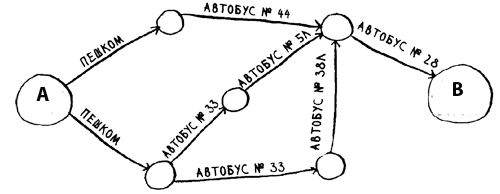
Найденный путь не обязательно окажется самым быстрым. Этот путь считается кратчайшим, потому что он состоит из наименьшего количества сегментов (три сегмента). Но предположим, с каждым сегментом связывается продолжительность перемещения. И тогда выясняется, что существует и более быстрый путь.
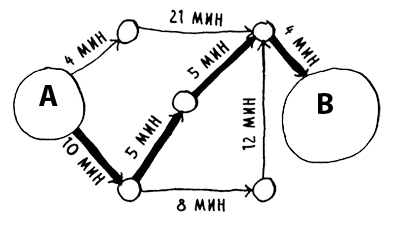
В шаге рассматривался поиск в ширину. Этот алгоритм находит путь с минимальным количеством сегментов (граф на первом рисунке). А если вы захотите найти самый быстрый путь (второй граф)? Быстрее всего это делается при помощи другого алгоритма, который называется алгоритмом Дейкстры.
Посмотрим, как этот алгоритм работает с графом.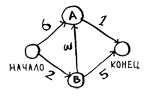
Каждому ребру назначается время перемещения в минутах. Алгоритм Дейкстры используется для поиска пути от начальной точки к конечной за кратчайшее возможное время.
Применив к этому графу поиск в ширину, вы получите следующий кратчайший путь.
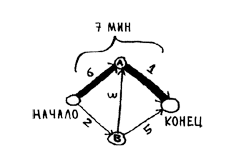
Этот путь занимает 7 минут. А может, существует путь, который займет меньше времени? Алгоритм Дейкстры состоит из четырех шагов:
- Найти узел с наименьшей стоимостью (то есть узел, до которого можно добраться за минимальное время).
- Обновить стоимости соседей этого узла.
- Повторять, пока это не будет сделано для всех узлов графа.
- Вычислить итоговый путь.
На следующем шаге рассмотрим шаги алгоритма более подробно.
