На этом шаге завершим рассмотрение шагов реализации алгоритма Дейкстры.
Шаг 3: повторяем!
Снова шаr 1: находим узел, для перехода к которому требуется наименьшее время. С узлом В работа закончена, поэтому наименьшую оценку времени имеет узел А.
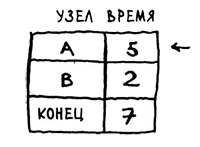
Снова шаr 2: обновляем стоимости соседей А.
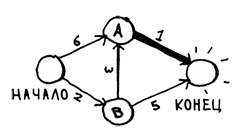
Путь до конечного узла теперь занимает всего 6 минут!
Алгоритм Дейкстры выполнен для каждого узла (выполнять его для конечного узла не нужно). К этому моменту вам известно следующее:
- Чтобы добраться до узла В, нужно 2 минуты.
- Чтобы добраться до узла А, нужно 5 минут.
- Чтобы добраться до конечного узла, нужно 6 минут.
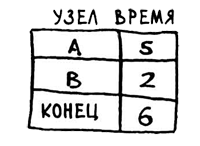
Последний шаг - вычисление итогового пути рассмотрим позже, а пока рассмотрим, как выглядит итоговый путь.
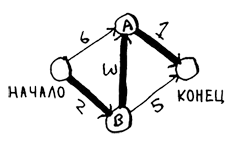
Алгоритм поиска в ширину не найдет этот путь как кратчайший, потому что он состоит из трех сегментов, а от начального узла до конечного можно добраться всего за два сегмента.
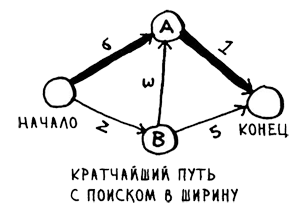
В предыдущих шагах мы использовали поиск в ширину для нахождения кратчайшего пути между двумя точками. Тогда под "кратчайшим путем" понимался путь с минимальным количеством сегментов. С другой стороны, в алгоритме Дейкстры каждому сегменту присваивается число (вес), а алгоритм Дейкстры находит путь с наименьшим суммарным весом.
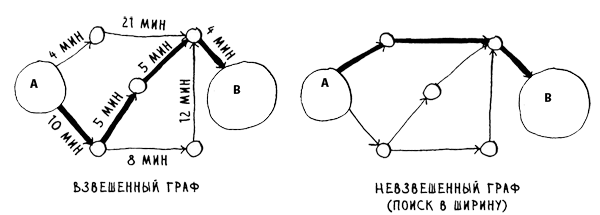
Алгоритм Дейкстры состоит из четырех шагов:
- Найти узел с наименьшей стоимостью (то есть узел, до которого можно добраться за минимальное время).
- Проверить, существует ли более дешевый путь к соседям этого узла, и если существует, обновить их стоимости.
- Повторять, пока это не будет сделано для всех узлов графа.
- Вычислить итоговый путь (об этом далее!).
На следующем шаге познакомимся с некоторыми терминами теории графов.
