На этом шаге познакомимся с некоторыми терминами теории графов.
Далее приведем еще несколько примеров применения алгоритма Дейкстры. Но сначала стоит немного разобраться с терминологией.
Когда вы работаете с алгоритмом Дейкстры, с каждым ребром графа связывается число, называемое весом (рис.1).
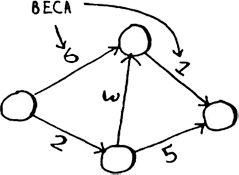
Рис.1. Вес ребра в графе
Граф с весами называется взвешенным графом. Граф без весов называется невзвешенным графом (рис.2).
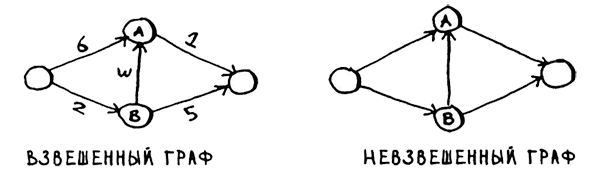
Рис.2. Взвешенный и невзвешенный графы
Для вычисления кратчайшего пути в невзвешенном графе используется поиск в ширину. Кратчайшие пути во взвешенном графе вычисляются по алгоритму Дейкстры. В графах также могут присутствовать циклы (рис.3).
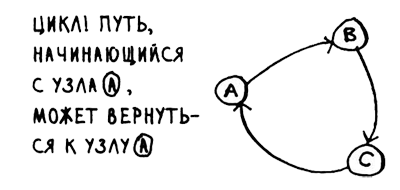
Рис.3. Цикл в графе
Это означает, что вы можете начать с некоторого узла, перемещаться по графу, а потом снова оказаться в том же узле. Предположим, нужно найти кратчайший путь в графе, содержащем цикл (рис. 4).
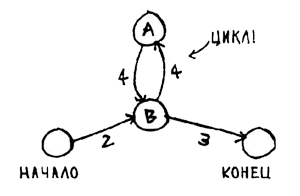
Рис.4. Поиск кратчайшего пути в графе с циклом
Есть ли смысл в перемещении по циклу? Что ж, вы можете использовать путь без прохождения цикла (рис.5):
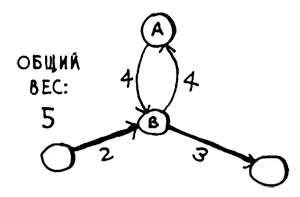
Рис.5. Не проходим по циклу
А можете пройти по циклу (рис.6):
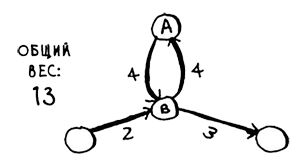
Рис.6. Проходим по циклу
Вы в любом случае оказываетесь в узле А, но цикл добавляет лишний вес. Вы даже можете обойти цикл дважды, если вдруг захотите.
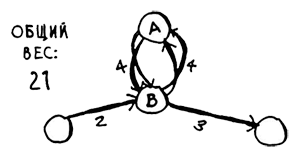
Рис.7. Проходим по циклу дважды
Но каждый раз, когда вы проходите по циклу, вы только увеличиваете суммарный вес на 8. Следовательно, путь с обходом цикла никогда не будет кратчайшим.
Рассмотрим направленные и ненаправленные графы (рис. 8):
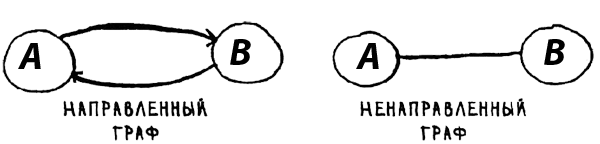
Рис.8. Направленные и ненаправленные графы
Само понятие ненаправленного графа означает, что каждый из двух узлов фактически ведет к другому узлу. А это цикл! (рис. 9)
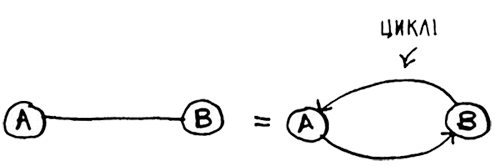
Рис.9. Ненаправленный граф = Цикл
В ненаправленном графе каждое новое ребро добавляет еще один цикл. Алгоритм Дейкстры работает только с направленными ациклическими графами, которые нередко обозначаются сокращением DAG (Directed Acyclic Graph).
На следующем шаге рассмотрим пример поиска кратчайшего пути в графе.
