На этом шаге рассмотрим результат применения алгоритма Дейкстры к графу с ребрами, имеющими отрицательный вес.
Если применить алгоритм Дейкстры к этому графу, Вася выберет неверный путь. Он пойдет по более длинному пути. Алгоритм Дейкстры не может использоваться при наличии ребер, имеющих отрицательный вес. Такие ребра нарушают работу алгоритма. Посмотрим, что произойдет, если попытаться применить алгоритм Дейкстры к этому графу. Все начинается с построения таблицы стоимостей (рис.1).
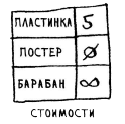
Рис.1. Таблица стоимостей
Теперь найдем узел с наименьшей стоимостью и обновим стоимости его соседей. В этом случае постер оказывается узлом с наименьшей стоимостью. Итак, в соответствии с алгоритмом Дейкстры, к постеру невозможно перейти более дешевым способом, чем с оплатой 0 рублей (а вы знаете, что это неверно!). Как бы то ни было, обновим стоимости его соседей (рис.2).
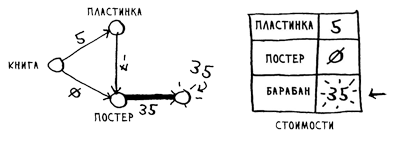
Рис.2. Таблица стоимостей после обновления
Получается , что теперь стоимость барабана составляет 35 тыс. рублей.
Перейдем к следующему по стоимости узлу, который еще не был обработан (рис. 3).
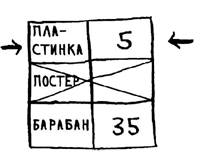
Рис.3. Обрабатываем следующий узел
Обновим стоимости его соседей (рис.4).
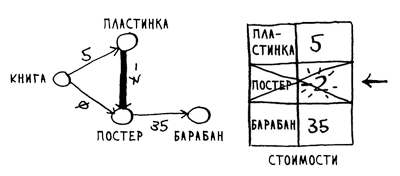
Рис.4. Очередная таблица стоимостей
Узел "постер" уже был обработан, однако вы обновляете его стоимость. Это очень тревожный признак - обработка узла означает, что к нему невозможно добраться с меньшими затратами. Но вы только что нашли более дешевый путь к постеру! У барабана соседей нет, поэтому работа алгоритма завершена. Ниже приведены итоговые стоимости (рис.5).
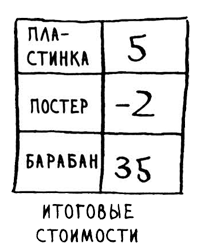
Рис.5. Итоговые стоимости
Чтобы добраться до барабанов, Васе потребовалось 35 тыс. рублей. Вы знаете, что существует путь, который стоит всего 33 тыс. рублей, но алгоритм Дейкстры его не находит. Алгоритм Дейкстры предположил, что, поскольку вы обрабатываете узел "постер", к этому узлу невозможно добраться быстрее. Это предположение работает только в том случае, если ребер с отрицательным весом не существует. Следовательно, использование алгоритма Дейкстры с графом, содержащим ребра с отрицательным весом, невозможно. Если вы хотите найти кратчайший путь в графе, содержащем ребра с отрицательным весом, для этого существует специальный алгоритм, называемый алгоритмом Беллмана - Форда.
На следующем шаге рассмотрим программную реализацию алгоритма Дейкстры.
