На этом шаге рассмотрим, как алгоритм Дейкстры реализуется в программном коде.
Рассморим пример программной реализации на следующем примере (рис.1).
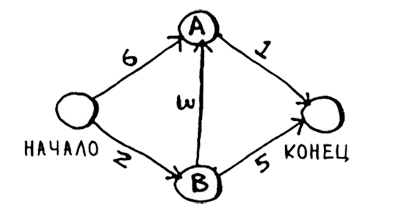
Рис.1. Граф
Для реализации этого примера понадобятся три хеш - таблицы (рис.2).
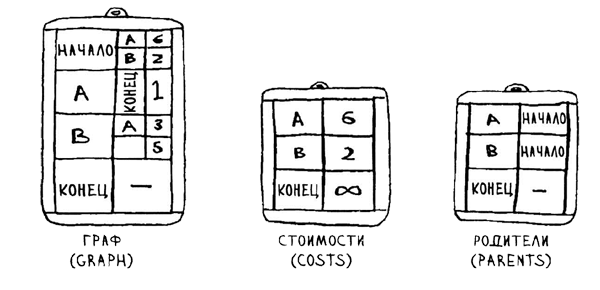
Рис.2. Хеш-таблицы
Хеш-таблицы стоимостей и родителей будут обновляться по ходу работы алгоритма. Сначала необходимо реализовать граф. Для этого будет использована хеш-таблица:
graph = {}Необходимо сохранить как соседей, так и стоимость перехода к соседу. Предположим, у начального узла есть два соседа, А и В (рис.3).
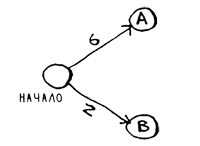
Рис.3. Соседи узла
Как представить веса этих ребер? Почему бы не воспользоваться другой хеш-таблицей?
graph ["start"] = {} graph ["start"] ["a"] = 6 graph ["start"] ["b"] = 2
Так можно представить эту хеш-таблицу (рис.4).
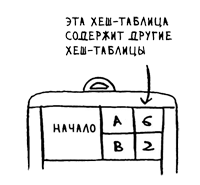
Рис.4. Хеш-таблица
Итак, graph["start"] является хеш-таблицей. Для получения всех соседей начального узла можно воспользоваться следующим выражением:
print (graph["start"].keys()) dict_keys(['b', 'a'])
Одно ребро ведет из начального узла в А, а другое - из начального узла в В. А если вы захотите узнать веса этих ребер?
print (graph["start"].["a"]) print (graph["start"].["b"]) 6 2
Включим в граф остальные узлы и их соседей:
graph["a"] = {} graph["a"]["fin"] = 1 graph["b"] = {} graph["b"]["a"] = 3 graph["b"]["fin"] = 5 graph["fin"] = {}
Полная хеш-таблица графа выглядит так (рис.5):
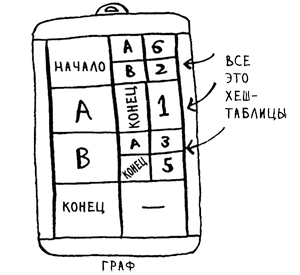
Рис.5. Полная хеш-таблица
На следующем шаге рассмотрим построение хеш-таблицы стоимостей всех узлов.
