На этом шаге рассмотрим решение задачи "Игра".

    Стартовые, промежуточные и финишные платформы естественно представлять вершинами графа, а трубы между ними — дугами. Однако данная задача слегка отличается по постановке от классической, поскольку здесь задан вес вершины: "...для каждой промежуточной платформы задано число С, равное максимальному количеству шариков, которые могут прокатиться по ней за время игры". Для перехода к классической постановке достаточно заменить такие вершины на дуги. При этом введенным дугам присваивается вес замененных вершин.

    Понятно, что должны появиться дополнительные вершины. Например, пусть в вершину 3 с весом X входит две дуги (1 → 3 и 2 → 3) и выходит две дуги (3 → 4 и 3 → 5), как показано на рис. 1:

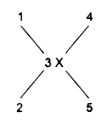
Рис.1. Исходное состояние вершины 3

    Мы добавляем вершину 6 и дугу 3 → 6 с весом X (рис. 2):

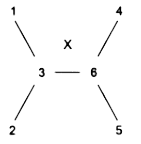
Рис.2. Преобразованный фрагмент графа

    Покажем теперь, как такой подход может быть реализован в данной задаче. Поскольку промежуточные платформы превращаются в дуги, то всего вершин становится на N2 больше, где N2 — количество промежуточных платформ.

readln (N1, N2, N3); {Количества платформ} 
All := N1 + N2 + N3; 
Finish := N1 + 2 * N2 + N3 + 1; {Платформы + сток} 

    Добавляем исток и связываем его с вершинами, соответствующими стартовым платформам. Пропускная способность дуг равна 1, поскольку по условию задачи на каждой из стартовых платформ находится шарик.

{Добавляем вершину-исток} 
ka[0] := N1; {Из истока - N дуг - к каждой стартовой платформе} 
for i := 1 to N1 do 
begin 
     a[0, i] := i; {Номер вершины, соединенной с истоком} 
     c[0, i] := 1; {на каждой из стартовых платформ - 1 шарик} 
end; 

    Для каждой промежуточной платформы с номером i добавляем две вершины с номерами N1 + i и all + i (где all = N1 + N2 + N3) соответственно. Добавляем также дугу между этим вершинами с пропускной способностью вершины.

{Добавляем дуги "внутри" промежуточных платформ} 
for i := 1 to N2 do {Для каждой промежуточной платформы} 
begin 
     readln (cn); {Читаем сколько шариков она выдержит} 
     a[N1 + i, 1] := all + i; {Добавляем дугу "внутри" этой платформы} 
     c[N1 + i, all + i] := cn; {Пропускная способность добавленной дуги} 
     ka[N1 + i] := 1; {Такая дуга всегда одна} 
end;

    Все входящие дуги от стартовых платформ будем строить в вершины N1 + i. По условиям задачи их пропускная способность не ограничена.

{Добавляем дуги от стартовых платформ к "началу" промежуточных} 
for i := 1 to N1 do 
begin 
	read(k); {Количество труб от платформы} 
	ka[i] := k; {Количество дуг из вершины i} 
	for j := 1 to k do {Для каждой трубы} 
	begin 
		read(a[i, j]); {Дуга из i в a[i,j]} 
		c[i, a[i, j]] := MaxP; {Ee пропускная            }
                                       {способность не ограничена} 
	end; 
end; 

    Все дуги от промежуточных платформ будем строить от вершин all + i — их пропускная способность также не ограничена.

{Добавляем дуги от "конца" промежуточных платформ к финишным платформам} 
for i := 1 to N2 do 
begin 
	read(k); {Количество труб от платформы} 
	ka[all + i] := k; {Количество дуг из вершины all+i} 
	for j := 1 to k do {Для каждой трубы} 
	begin 
		read (np); {Номер "целевой" платформы} 
		a[all + i, j] := np; {Дуга из N1+2*i в a[i,j]} 
		c[all + i, a[all + i, j]] := MaxP; {Ee пропускная            }
                                                   {способность не ограничена} 
	end; 
end; 

    Добавляем вершину-сток с дугами к ней от всех финишных платформ. Веса этих дуг равны 1, поскольку на каждой из финишных платформ может оказаться не более одного шарика.

{Добавляем вершину-сток} 
N := N1 + N2; {Стартовый номер финишных платформ} 
for i := 1 to N3 do {Для каждой финишной платформы} 
begin 
	ka[N + i] := 1;
	= a[N + i, 1] :-Finish ; {Одна дуга на каждую финишную платформу} 
	c[N + i, Finish] := 1; {Ha каждой из финишных платформ - не более 1 шарика} 
end;

    Для вывода ответа на поставленный в задаче вопрос "Какое максимальное количество шариков может оказаться на финишных платформах в результате игры?" после построения максимального потокадостаточно просуммировать количество шариков, выкатившихся из истока на стартовые платформы:

Max := 0; 
for i := 1 to N1 do   	Max := Max + f[0, i]; 
writeln(Max); 

    На следующем шаге рассмотрим понятие минимального остовного дерева.

Предыдущий шаг Содержание Следующий шаг