На этом шаге мы познакомимся с правилами выполнения действий с двоичными числами.
Так как компьютер может различить только нулевое и единичное состояние бита, то он работает в системе счисления с основанием 2 или в двоичной системе. Бит получил свое название от английского Binary digit (двоичная цифра).
Сочетанием двоичных цифр (битов) можно представить любое значение. Значение двоичного числа определяется относительной позицией каждого бита и наличием единичных битов. Ниже показано восьмибитовое число, содержащее все единичные биты:
позиционные веса: 128 64 32 16 8 4 2 1
включенные биты: 1 1 1 1 1 1 1 1
Самая правая цифра имеет весовое значение 1, следующая цифра влево - 2, следующая - 4 и т.д. Общая сумма для восьми единичных битов в данном случае составит 255 (1+2+4+8+16+32+64+128=255).
Компьютер выполняет арифметические действия только в двоичном формате. Поэтому, программируя на языке Ассемблер, необходимо знать правила сложения в двоичной системе счисления. Напомним их:
0 + 0 = 0
1 + 0 = 1
1 + 1 = 10 .
Проиллюстрируем использование этих правил на конкретном примере.
Пример: сложить числа 65 и 42, представленные в двоичной системе счисления. В десятичной системе счисления все осуществляется достаточно просто: 65+42=107.
Для сложения этих чисел в двоичной системе счисления нужно сначала перевести их в эту систему:
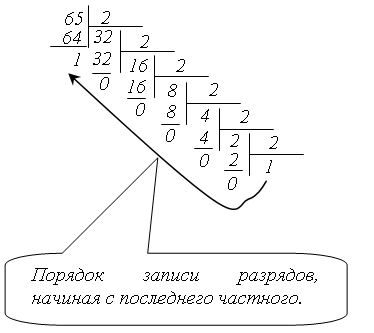
Рис.1. Алгоритм перевода числа из десятичной в двоичную систему счисления
Таким образом, получаем: 6510 = 010000012. Обратите внимание на то, что ведущий ноль в двоичном представлении числа добавлен для дополнения двоичного представления до восьми бит.
Аналогично: 4210 = 001010102. Выполним сложение этих чисел:
+01000001
00101010
--------
01101011
Можно убедиться, что 011010112=10710:
0*27+1*26+1*25+0*24+1*23+0*22+1*21+1*20 = 64+32+8+2+1 = 107.
Мы рассмотрели сложение чисел в компьютере. А как же осуществляется вычитание? Для выполнения операции вычитания оно заменяется сложением, а в качестве второго слогаемого берется противоположное число. Например, пусть надо выполнить вычитание: 65 - 42. Заменим его сложением: 65 + (-42). Но как получить соответствующее двоичное отрицательное число? Этот вопрос мы сейчас рассмотрим.
Все представленные выше двоичные числа имеют положительные значения, что обозначается нулевым значением самого левого (старшего) разряда. Отрицательные двоичные числа содержат единичный бит в старшем разряде. Для получения отрицательного двоичного числа можно использовать следующий алгоритм:
- взять соответствующее положительное число и инвертировать его биты (1 заменить на 0 и наоборот);
- к полученному числу прибавить 1.
Приведем пример использования рассмотренного алгоритма.
Пример 1. Получить двоичное представление числа -65. Напомним, что 6510 = 010000012. Инвертируем биты: 10111110. К полученному числу прибавим 1: 10111110+1=10111111. Убедимся в правильности представления. Сумма +65 и -65 должна составить нуль:
+01000001
10111111
--------
(1) 00000000
Все восемь бит имеют нулевое значение. Пока будем считать, что полученная единица, перенесенная влево, потеряна.
Это правило позволяет выполнять вычитание чисел в двоичной системе счисления: вычитание заменяется сложением и в качестве второго слагаемого берется отрицательное число.
Пример 2. Вычесть из 65 число 42. Двоичное представление для 42 - это 00101010, а для -42 двоичное представление будет следующим - 11010110:
+65 = 01000001
(-42) = 11010110
----- --------
23 (1)00010111
Пример 3. Какое значение необходимо прибавить к двоичному числу 00000001, чтобы получить число 00000000? В терминах десятичного счисления ответом будет число -1. Для двоичного счисления это число 11111111:
+00000001
11111111
--------
(1) 00000000
В заключение приведем фрагмент уменьшающегося ряда чисел в двоичном представлении:
. . . .
3 00000011
2 00000010
1 00000001
0 00000000
-1 11111111
-2 11111110
-3 11111101
. . . .
На следующем шаге мы познакомимся с шестнадцатеричным представлением чисел.
