На этом шаге мы рассмотрим построение идеально сбалансированных бинарных деревьев.

    Пусть требуется построить бинарное дерево с n узлами и минимальной высотой (максимально "ветвистое" и "низкое"). Такие деревья имеют большое практическое значение, так как их использование сокращает машинное время, требуемое на выполнение различных алгоритмов.

Определение.

Бинарное дерево назовем идеально сбалансированным, если для каждой его вершины количество вершин в левом и правом поддереве различаются не более чем на 1.

    Изобразим несколько идеально сбалансированных деревьев:

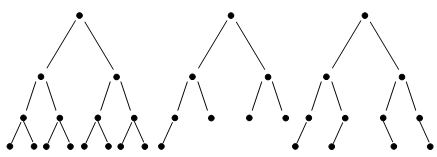
Рис.1. Примеры идеально сбалансированных бинарных деревьев

Теорема.

Длина внутреннего пути в идеально сбалансированном дереве, содержащем n вершин, не превосходит величины: (n+1)[log₂n] - 2 * 2^[log₂n] - 2

Доказательство.

Ясно, что только одна вершина (а именно корень) может находиться на нулевом расстоянии от корня; не более двух вершин могут находиться на расстоянии 1 от корня; не более четырех вершин могут находиться от корня на расстоянии, равном 2 и т.д. Мы видим, что длина внутреннего пути всегда не больше суммы первых n членов ряда:

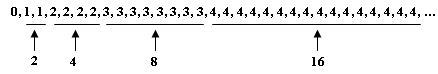
Рис.2. Длина внутреннего пути

    Взгляните на следующее соотношение:

    k    1 2 3 4 5 6 7 8 9 10 11 12 13 ...
[log2k]  0 1 1 2 2 2 2 3 3  3  3  3  3  ...

    Теперь легко понять, что сумма первых n членов равна:

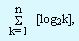
символы [ ] - обозначение операции выделения целой части числа.

    В [2, с.74] показывается, что:

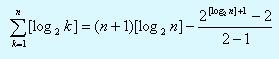
откуда и следует утверждение теоремы.

    Алгоритм построения идеально сбалансированного дерева при известном числе вершин n лучше всего формулируется с помощью рекурсии [1,с.226]. При этом необходимо лишь учесть, что для достижения минимальной высоты при заданном числе вершин, нужно располагать максимально возможное число вершин на всех уровнях, кроме самого нижнего. Это можно сделать очень просто, если распределять все поступающие в дерево вершины поровну слева и справа от каждой вершины.

    Суть алгоритма [1,с.226]:

• взять одну вершину в качестве корня.
• построить левое поддерево с nl = n DIV 2 вершинами тем же способом.
• построить правое поддерево с nr = n-nl-1 вершинами тем же способом.

    Оформим описанный алгоритм в виде рекурсивной функции:

node *Tree (int n, node **p)
// Построение идеально сбалансированного дерева с n вершинами.
// *p - указатель на корень дерева.
{
  node *now;
  int x,nl,nr;

  now = *p;
  if (n==0) *p = NULL;
  else
  { nl = n/2; nr = n - nl - 1; cin>>x;
    now = new(node);(*now).Key = x; 
    Tree (nl,&((*now).Left)); Tree (nr,&((*now).Right)); *p = now;}
}

#include<iostream.h>
struct node
{
  int Key;
  int Count;
  node *Left;
  node *Right;
};

class TREE
{
  private:
    node *duk; //Корень дерева.
  public:
    TREE() { duk = NULL; }
    node **GetDuk() { return &duk; }
    node *Tree (int, node **); 
    void Vyvod (node **, int);
};

void main ()
{
  TREE A;
  int n;

  cout<<"Введите количество вершин -...\n"; cin>>n;
  cout<<"Вводите ключи...\n";
  A.Tree (n,A.GetDuk()); A.Vyvod (A.GetDuk(),0);
}
   
node *TREE::Tree (int n,node **p)
// Построение идеально сбалансированного
//           дерева с n вершинами.
// *p - указатель на корень дерева.
{
  node *now;
  int x,nl,nr;
     
  now = *p;
  if  (n==0) *p = NULL;
  else
  {
    nl = n/2; nr = n - nl - 1;
    cin>>x;
    now = new(node);
    (*now).Key = x;
    Tree (nl,&((*now).Left));
    Tree (nr,&((*now).Right));
    *p = now;
  }
}

void TREE::Vyvod (node **w,int l)
// Изображение бинарного дерева, заданного
// указателем *w на экране дисплея.
{
  if  (*w!=NULL)
  {
    Vyvod (&((**w).Right),l+1);
    for  (int i=1; i<=l; i++) cout<<"   ";
    cout<<(**w).Key<<endl;
    Vyvod (&((**w).Left),l+1);
  }
}

    Отметим простоту и ясность этой программы, достигнутые благодаря использованию рекурсивных процедур. Очевидно, что рекурсивные алгоритмы особенно уместны, когда программа должна обрабатывать данные, структура которых определена рекурсивно.

    Предположим, например, что имеется следующий набор ключей для построения дерева с 21 вершиной: 8, 9, 11, 15, 19, 20, 21, 7, 3, 2, 1, 5, 6, 4, 13, 14, 10, 12, 17, 16, 18. Результат работы программы следующий:

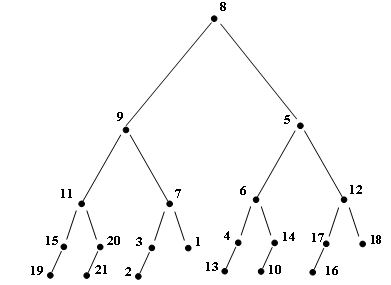
Рис.3. Результат работы приложения

    Одно "но": при формировании идеально сбалансированного дерева ключи необходимо вводить в отсортированном по возрастанию (по убыванию) виде. В этом случае можно построить достаточно простой алгоритм поиска в идеально сбалансированном дереве вершины с заданным ключом.

    На следующем шаге мы разберем балансированные по высоте деревья.

Предыдущий шаг Содержание Следующий шаг