На этом шаге мы рассмотрим деревья Фибоначчи.

Hаиболее асимметpичное АВЛ-деpево T_h высоты h имеет наиболее асимметpичное АВЛ-деpево T_h-1 высоты h-1 в качестве одного из своих поддеpевьев и наиболее асимметpичное АВЛ-деpево высоты h-2 в качестве дpугого. Подобные деpевья называются деpевьями Фибоначчи.

Дерево Фибоначчи несколько больше напоминает реальный куст, чем рассматривавшиеся ранее деревья, возможно, потому, что многие природные процессы удовлетворяют закону Фибоначчи.

Приведем формальное определение дерева Фибоначчи.

Дерево Фибоначчи порядка k определяется следующим образом [2, с.493; 6, с.274].

если k=0, то дерево Фибоначчи пусто;
если k=1, то дерево Фибоначчи состоит из единственного узла, ключ которого содержит 1;
если k >=2, то корень дерева Фибоначчи содержит ключ F_k, левое поддерево есть дерево Фибоначчи порядка k-1, правое поддерево есть дерево Фибоначчи порядка k-2 с ключами в узлах, увеличенными на F_k.

Здесь F_k - k-е число Фибоначчи: F₀=1, F₁=1, F₂=2, F₃=3, F₄=5, F₅=8, F₆=13, ... (Заметим, что в математике рядом Фибоначчи называется последовательность u₁, u₂, ..., u_n,..., в которой u₁=1, u₂=1, u_n=u_n-1+u_n-2 для любого n>2, а члены этой последовательности - числами Фибоначчи.)

Изобpазим несколько деpевьев Фибоначчи pазной высоты:

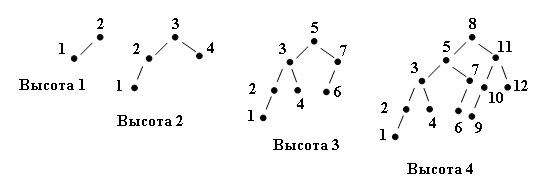
Рис.1. Деревья Фибоначчи

Заметим, что ключи, соответствующие преемникам каждого узла, отличаются от ключа в этом узле на одну и ту же величину, а именно - на число Фибоначчи. Так, 5=8-F₄, 11=8+F₄.

Пример 1. Построение дерева Фибоначчи.

#include <iostream.h>

struct Node
{
	int   Key;
	Node* Left;
	Node* Right;
};

class Tree
{
  private:
		Node* Root; //Указатель на корень дерева.
  public:
		Tree() { Root = NULL; };
		void PrintTree (Node*, int);
		void FibonTree1 (int, Node**);
		void FibonTree2 (Node**,int *);
		Node** GetTree() {return &Root;};
		Node* GetTree1() {return Root;};
};

// ------------ РЕАЛИЗАЦИЯ МЕТОДОВ КЛАССА ----------

void Tree::PrintTree (Node* W, int l)
{
  int i;

  if  (W!=NULL)
  {
	 PrintTree (W->Right,l+1);
	 for (i=1;i<=l;i++) cout << "   ";
	 cout << W->Key << endl;
	 PrintTree (W->Left,l+1);
  }
}

void Tree::FibonTree1 (int k, Node** T)
// Построение дерева Фибоначчи порядка k с незаполненными
// полями Key узлов.
{
  if ( k==0)  (*T) = NULL;
  else
	if ( k==1 )
	 {
		(*T) = new (Node);
		(*T)->Left = (*T)->Right = NULL;
	 }
	else
	 {
		(*T) = new (Node);
		FibonTree1 (k-1,&((*T)->Left));
		FibonTree1 (k-2,&((*T)->Right));
	 }
}

void Tree::FibonTree2 (Node** T,int* i)
// Заполнение поля Key узлов дерева Фибоначчи.
{
  if ( (*T)!=NULL )
  {
	  FibonTree2 (&((*T)->Left),i);
	  (*T)->Key = (*i); (*i)++;
	  FibonTree2 (&((*T)->Right),i);
  }
}

void main()
{
  Tree A;
  int k;
  cout << "Вводите k...";
  cin >> k;
  int i = 1; // Инициализация самого левого ключа дерева.
  A.FibonTree1 (k,A.GetTree());
  A.FibonTree2 (A.GetTree(),&i);
  A.PrintTree (A.GetTree1(),0);

}

Текст этой программы можно взять здесь.

Результат работы программы изображене на рисунке 2:

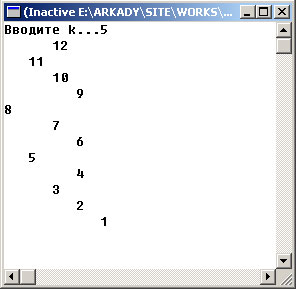
Рис.2. Результат работы приложения

Дадим следующее опpеделение "показателю сбалансиpованности" узла для бинарных деpевьев:

   показатель сбалансиpованности узла  =
           = высота пpавого поддеpева - высота левого поддеpева.

В деpеве Фибоначчи для всех узлов (за исключением листьев) показатель сбалансиpованности pавен или +1 или -1.

Балансированные по весу деревья (WB-деревья) [3, с.220-221; 4,с.269-277] - это класс бинарных деревьев, в которых ограничения на высоты поддеревьев заменено ограничением на число вершин в поддеревьях. Хотя они базируются на других принципах и не сравнимы с АВЛ-деревьями - поскольку эти классы не содержат друг друга и практически не пересекаются, - они обладают схожими свойствами. От АВЛ-деревьев WB-деревья отличаются тем, что содержат параметр, который может изменяться так, что можно произвольно ограничивать длину самого длинного пути из корня в висячую вершину за счет увеличения дисбаланса.

Пусть T_n=(T_l,v,T_r) есть бинарное дерево с корнем v, где T_l и T_r - бинарные поддеревья с n_l и n_r вершинами соответственно, n_l+n_r=n-1, n_l>=0, n_r>=0.

Корневым балансом b(T_n) бинарного дерева T_n=(T_l,v,T_r) называется величина


             n_l+1
     b(T_n)=-------, n >= 1
             n+1

Заметим, что b(T_n) определяет относительное число узлов в левом поддереве дерева T_n и для корневого баланса всегда выполняется неравенство


    0 < b(T_n) < 1   .

Дерево T_n называется балансированным по весу с балансом A, 0< A < 1/2, если оно удовлетворяет следующим условиям:

A <= b(T_n) <= 1 - A;
T_l, T_r - балансированные по весу деревья с балансом A.

Класс бинарных деревьев с балансом A будем обозначать через WB[A]. Пустое бинарное дерево T₀, по определению, входит в WB[A] для любого A. Класс WB[A] становится все более ограниченным по мере того, как A меняется от 0 до 1/2.

Случай 1/2 означает, что

либо левое и правое поддеревья каждой вершины содержат одинаковое число вершин, поэтому классу WB[1/2] принадлежат полностью балансированные деревья с n=2^k-1 вершинами,
либо нам встретилось дерево вида

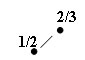
Рис.3. Дерево специального вида

В примерах на рисунках ниже баланс каждого поддерева дерева Фибоначчи выписан рядом с корнем каждого поддерева; минимум этих балансов - это максимальное A, при котором данное дерево принадлежит WB[A].

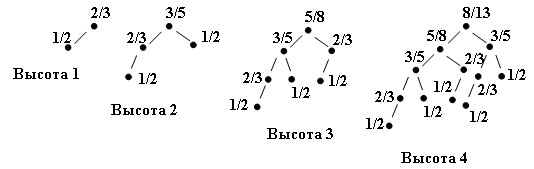
Рис.4. Деревья Фибоначчи

Пример 2.

#include <iostream.h>

struct Node
{
	int   Key;
	float Bal; //Корневой баланс.
	Node* Left;
	Node* Right;
};

class Tree
{
  private:
		Node* Root;   //Указатель на корень дерева.
		float BalMin; //Баланс дерева Фибоначчи.
  public:
		Tree() { Root = NULL; BalMin = 1;};
		void PrintTreeBal (Node*, int);
		void FibonTree1 (int, Node**);
		void FibonTree2 (Node**,int *);
		int  NodeCount (Node*);
		Node** GetTree() {return &Root;};
		Node* GetTree1() {return Root;};
		int GetBalMin() {return BalMin;};
};

// ------------ РЕАЛИЗАЦИЯ МЕТОДОВ КЛАССА ----------

void Tree::PrintTreeBal (Node* W, int l)
// Вывод бинаpного деpева на экpан дисплея с указанием
// показателей баланса весов для каждого узла деpева.
{
  int i;

  if  (W!=NULL)
  {
	 PrintTreeBal (W->Right,l+1);
	 for (i=1;i<=l;i++) cout << "   ";
	 W->Bal = (float)(NodeCount (W->Left)+1)/(float)(NodeCount (W)+1);
	 if ( BalMin > W->Bal) BalMin = W->Bal;
	 cout << W->Key << '('<< W->Bal << ')' << endl;
	 PrintTreeBal (W->Left,l+1);
  }
}

void Tree::FibonTree1 (int k, Node** T)
// Построение дерева Фибоначчи порядка k с незаполненными
// полями Key узлов.
{
  if ( k==0)  (*T) = NULL;
  else
	if ( k==1 )
	 {
		(*T) = new (Node);
		(*T)->Left = (*T)->Right = NULL;
	 }
	else
	 {
		(*T) = new (Node);
		FibonTree1 (k-1,&((*T)->Left));
		FibonTree1 (k-2,&((*T)->Right));
	 }
}

void Tree::FibonTree2 (Node** T,int* i)
// Заполнение поля Key узлов дерева Фибоначчи.
{
  if ( (*T)!=NULL )
  {
	  FibonTree2 (&((*T)->Left),i);
	  (*T)->Key = (*i); (*i)++;
	  FibonTree2 (&((*T)->Right),i);
  }
}

int Tree::NodeCount (Node* T)
// Подсчет количества узлов в бинаpном деpеве T.
{
  if ( T==NULL ) return 0;
  else
	 if  (T->Left==NULL && T->Right==NULL) return 1;
	 else
		  return NodeCount(T->Right)+NodeCount(T->Left)+1;
}

void main()
{
  Tree A;
  int k;
  cout << "Вводите k...";
  cin >> k;
  //Построение дерева Фибоначчи.
  int i = 1; // Инициализация самого левого ключа дерева.
  A.FibonTree1 (k,A.GetTree());
  A.FibonTree2 (A.GetTree(),&i);
  //Вывод дерева Фибоначчи, корневых балансов и баланса дерева.
  A.PrintTreeBal (A.GetTree1(),0);
  cout << "\nБаланс дерева Фибоначчи: " << A.GetBalMin();
}

Текст этой программы можно взять здесь.

После нескольких экспериментов с программой из примера 2 можно высказать гипотезу о том, что деревья Фибоначчи принадлежат классу WB[1/2].

Попробуйте доказать этот факт самостоятельно!

Заметим, что в монографии [3,с.221] утверждается, что деревья Фибоначчи принадлежат классу WB[1/3]. Дело в том, что автор использует "чуть-чуть" другое дерево Фибоначчи, которое совпадает с нашим, если зеркально отобразить его относительно вертикальной оси, проходящей через корень!

Для оценки наибольшей высоты дерева Фибоначчи воспользуемся теоремой.

Теорема [3, с.222].: Высота дерева T_n из класса WB[A] не превышает

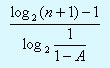
Отсюда следует, что высота дерева Фибоначчи не превышает log₂(n+1)-1.

⁽¹⁾ Кнут Д. Искусство программирования для ЭВМ. Т.3: Сортировка и поиск. - M.: Мир, 1978. - 844 с.
⁽²⁾ Вирт H. Алгоритмы и структуры данных. - М.: Мир, 1989. - 360 с.
⁽³⁾ Евстигнеев В.А. Применение теории графов в программировании. -М.: Hаука, 1985. - 352 с.
⁽⁴⁾ Рейнгольд Э., Hивергельт Ю., Део H. Комбинаторные алгоритмы. Теория и практика. - М.: Мир, 1980. - 476 с.

Со следующего шага мы начнем рассматривать алгоритмы балансировки.

Предыдущий шаг Содержание Следующий шаг