На этом шаге мы рассмотрим применение рекурсии.
При описании методов можно использовать рекурсию. При рекурсии в теле метода вызывается этот же метод (но обычно с другим значением аргумента или аргументов). Такой подход позволяет создавать эффектные коды. Правда, "эффектный" не всегда означает "эффективный". Классическим примером использования рекурсии является программа для вычисления факториала числа (с использованием рекурсии). Чтобы понять, как организуется программный код, имеет смысл учесть, что факториал числа n! = 1 * 2 * 3 * ... * (n - 1) * n может быть представлен в виде n! = (n - 1)! * n - то есть факториал для числа n может быть представлен как факториал для числа n - 1, умноженный на n. Программный код статического метода, вычисляющего факториал числа (переданного аргументом методу), может быть таким:
static int factorial (int n){ if ( n == 1 ) return 1; else return n * factorial(n-1); }
Основу тела метода factorial() составляет условный оператор, в котором проверяется равенство единице аргумента метода n (условие n==1). Если это так, то результатом метода возвращается значение 1 (по определению 1! = 1). Если условие ложно, то результатом метода возвращается значение выражения n*factorial(n-1). В этом выражении использован вызов метода factorial(), но с аргументом n-1. Как это работает? Достаточно просто. Допустим, метод factorial() вызывается с аргументом 1. Тогда при проверке условия в условном операторе оно окажется истинным и результатом метода возвращается значение 1. Теперь предположим, что метод factorial() вызывается с аргументом, отличным от 1 - например, с аргументом 3. При проверке условия оно окажется ложным, и результатом метода возвращается значение выражения 3*factorial(2). Но перед тем как вернуть значение, его необходимо вычислить. А для этого снова вызывается метод factorial(), но с аргументом 2. Проверяется условие, оно ложное, и значение выражения factorial(2) вычисляется как 2*factorial(1). Снова вызывается метод factorial(), но с аргументом 1. А мы уже знаем, что значением выражения factorial(1) является 1. Тогда значение выражения factorial(2) равно 2, а значение выражения factorial(3) равно 6. Понятно, что, чем больше значение аргумента метода, тем длиннее цепочка вызовов метода factorial().
Аналогичным образом с использованием рекурсии описываются и другие методы. Например, так может выглядеть программный код для статического метода, вычисляющего число в последовательности Фибоначчи по его номеру (аргумент метода):
static int fibs(int n){ if ( n == 1 || n == 2 ) return 1; else return fibs(n-1) + fibs(n-2); }
Здесь мы учли тот факт, что при значениях аргумента 1 или 2 (первое или второе число в последовательности) метод должен возвращать значение 1. Во всех остальных случаях число с номером n вычисляется как сумма двух предыдущих чисел. Поэтому программный код метода fibs() организован в виде условного оператора, в котором проверяется условие n==1||n==2 (аргумент n равен 1 или 2). Если так, то результатом метода возвращается значение 1. Если условие ложно, то результатом метода возвращается значение выражения fibs(n-1) + fibs(n-2), в котором вызывается метод fibs() (причем дважды).
Рекурсию можно использовать даже там, где ее, на первый взгляд, не может быть вообще. Например, задача на вычисление суммы натуральных чисел. Допустим, нам нужно вычислить сумму S(n) = 1 + 2 + 3 + ... + (n - 1) + n. Но ее можно представить в виде S(n) = n + S(n - 1) - то есть сумма n натуральных чисел есть сумма n - 1 натуральных чисел плюс число n. Значит, статический метод для вычисления суммы натуральных чисел с использованием рекурсии можно описать так:
static int sum(int n){ if ( n == 0 ) return 0; else return n + sum(n-l); }
To есть если аргумент метода равен 0, то результатом является значение 0. В противном случае значение выражения sum(n) вычисляется как n+sum(n-l). В примере ниже представлена программа со статическими методами, в описании которых использована рекурсия.
using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace pr72_1 { class Program { // Метод для вычисления факториала числа: static int factorial(int n){ if ( n == 1 ) return 1; else return n * factorial(n-1); } // Метод для вычисления чисел Фибоначчи: static int fibs(int n){ if( n == 1 || n == 2 ) return 1; else return fibs(n-1) + fibs(n-2); } // Метод для вычисления суммы чисел: static int sum(int n){ if ( n == 0 ) return 0; else return n + sum(n-1); } // Метод для отображения содержимого массива: static void show(int[] a, int k){ // Отображение значения элемента массива: Console.Write(a[k] + " "); // Если элемент в массиве последний: if ( k == a.Length - 1 ){ Console.WriteLine(); } // Если элемент в массиве не последний: else { // Рекурсивный вызов метода: show(a, k + 1); } } // Перегрузка метода для отображения // содержимого массива: static void show(int[] a){ // Вызов версии метода с двумя аргументами: show(a, 0); } // Главный метод программы: static void Main() { Console.WriteLine("Факториал числа:"); for(int k=1; k <= 10; k++){ // Вычисление факториала числа: Console.WriteLine(k + "!=" + factorial(k)); } Console.WriteLine("Числа Фибоначчи:"); for(int k=1; k <= 10; k++) { // Вычисление чисел Фибоначчи: Console.Write(fibs(k) + " "); } Console.WriteLine(); Console.Write("Сумма чисел от 1 до 100: "); Console.WriteLine(sum(100)); // Числовой массив: int[] A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21}; Console.WriteLine("Числовой массив:"); // Отображение всех элементов массива: show(A); Console.WriteLine("Элементы, начиная с третьего:"); // Отображение элементов, начиная с третьего: show(A, 2); // Задержка: Console.ReadLine(); } } }
Результат выполнения программы представлен ниже:
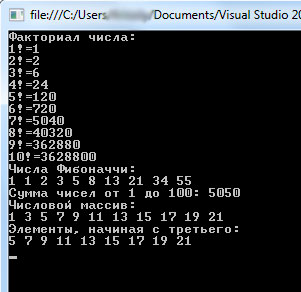
Рис.1. Результат выполнения программы
В программе, кроме уже описанных методов, использовался метод show() для отображения массива. В нем также задействована рекурсия. Аргументов у метода два:
- отображаемый массив (объявлен как int[] а) и
- индекс элемента, начиная с которого выполняется отображение элементов массива (соответствующий аргумент объявлен как int k).
Console.Write(а[k] +" ") ;
Console.WriteLine();
show(а, k+1);
Если мы хотим отобразить значения всех элементов массива, то нам необходимо вызвать метод show() со вторым нулевым аргументом. Мы для удобства переопределяем метод show(), описав версию метода без второго аргумента (первый аргумент - отображаемый массив). В описании версии метода show() с одним аргументом есть всего одна команда
show(а, 0); ,
При перегрузке метода show() о рекурсии речь не идет. Дело в том, что когда в теле версии метода show() с одним аргументом вызывается версия метода show() с
двумя аргументами, то фактически вызывается другой метод (просто название у него такое же). Это не рекурсивный вызов. При рекурсивном вызове метод вызывает сам себя.
В главном методе программы проиллюстрирована работа статических методов. В частности, там для чисел от 1 до 10 вычисляется факториал, вычисляется последовательность чисел Фибоначчи, а также отображается содержимое одномерного целочисленного массива. Во всех этих случаях используются методы, реализованные на основе рекурсии.
На следующем шаге мы рассмотрим методы с произвольным количеством аргументов.
