На этом шаге мы приведем еще один пример использования статических методов класса.

    Еще один, на этот раз "математический" пример с использованием статических полей и методов представлен ниже. В программе описан класс MyMath, в котором есть статические методы для вычисления значений синуса и экспоненты. В классе также имеется константное статическое поле, значение которого определяет иррациональное число π.

Что касается статических полей, то нередко они используются как статические константы: для такого поля указывается идентификатор типа (и если нужно - спецификатор уровня доступа), но вместо ключевого слова static указывается идентификатор const. Причина в том, что константные поля по умолчанию реализуются как статические. Значение константного поля указывается при объявлении и впоследствии не может быть изменено.

Для вычисления экспоненты используется следующее выражение: ехр(х) ≈ 1 + х + x²/2! + x³/3! + ... + xⁿ/n! = Σⁿ_k=0x^k/k!. В программе описывается статический метод для вычисления суммы Σⁿ_k=0q_k = q₀ + q₁ + ... + q_n, где при заданном значении аргумента х слагаемые в сумме вычисляются как q_k= x^k/k! . Сумма вычисляется с помощью оператора цикла, в котором после прибавления к сумме очередного слагаемого рассчитывается слагаемое для следующей итерации. При этом мы исходим из того, что если вычислена добавка q_k для текущей итерации, то добавка q_k+1 для следующей итерации вычисляется как q_k+1 = q_k * x/(k+1) (легко проверить, что если q_k = x_k/k! и q_k+1 = x_k+1/(k+1)!, то q_k+1/q_k = x/(k+1)).

    Аналогичным образом вычисляется синус: используется формула sin(x) = x - x³/3! + x⁵/5! - x⁷/7! + ... + (-1)ⁿx²ⁿ⁺¹/(2n+1)! = Σⁿ_k=0(-1)^kx_2k+1/(2k+1)!. Подход используем тот же, что и при вычислении экспоненты - то есть вычисляется сумма вида Σⁿ_k=0q_k = q₀ + q₁ + ... + q_n, но на этот раз q_k= (-1)^kx^2k+1/(2k+1)!, q_k+1= (-1)^(k+1)x^2k+3/(2k+3)!, q_k+1/q_k = -x²/((2k+2)(2k+3)) и тогда q_k+1 = q_k*(-1)x²/((2k+2)(2k+3)).

    Для определения значения параметра n (верхняя граница в суммах, через которые вычисляется синус и экспонента) в программе (в соответствующем классе) объявлено статическое целочисленное поле. А значение π=3,141592 определяется через статическую константу.

    Проанализируем представленный ниже программу.

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace pr87_1
{
    // Класс со статическими методами и полями: 
    class MyMath {
        // Константное поле (число "пи"): 
        public const double Pi = 3.141592;
        // Закрытое статическое поле (граница суммы): 
        private static int N = 100;
        // Статический метод для вычисления экспоненты: 
        public static double exp(double x) {
            // Сумма и добавка к сумме: 
            double s = 0, q = 1;
            // Вычисление суммы: 
            for(int k = 0; k <= N; k++) {
                s += q;	// Прибавление добавки к сумме
                q *= x/(k + 1); // Добавка для следующей итерации
            }
            // Результат: 
            return s;
        }

        // Статический метод для вычисления синуса: 
        public static double sin(double x) {
            // Сумма и добавка к сумме: 
            double s = 0, q = x;
            // Вычисление суммы: 
            for(int k = 0; k <= N; k++) {
                s += q;	// Прибавление добавки к сумме
                // Добавка для следующей итерации: 
                q *= (-1) * x * x / ( 2 * k + 2) / (2 * k + 3);
            }
            // Результат: 
            return s;
        }
    }

    // Главный класс:
    class Program
    {
        static void Main()
        {
            // Аргумент для статических методов: 
            double z = 1;
            // Вычисление экспоненты:
            Console.WriteLine("ехр({0}) = {1}", z, MyMath.exp(z));
            // Контрольное значение:
            Console.WriteLine("Контрольное значение: {0}", Math.Exp(z));
            // Новое значение аргумента: 
            z = MyMath.Pi/4;
            // Вычисление синуса:
            Console.WriteLine("sin({0}) = {1}", z, MyMath.sin(z));
            // Контрольное значение:
            Console.WriteLine("Контрольное значение: {0}", Math.Sin(z));
            // Задержка:
            Console.ReadLine();
        }
    }
}

    Результат выполнения программы такой.

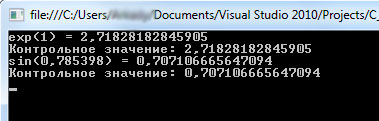
Рис.1. Результат выполнения программы

    Мы описываем класс MyMath, в котором описаны статические методы ехр() и sin() для вычисления соответственно экспоненты и синуса. Оба метода реализованы по общему принципу: объявляются две локальные числовые переменные s и q. В первую записывается значение для суммы, через которую вычисляется экспонента или синус, а во вторую заносится значение добавки к сумме. Начальное значение суммы в обоих случаях нулевое. При вычислении экспоненты первая добавка единичная, а для синуса первая добавка к сумме равна значению аргумента, переданного методу.

    Сумма вычисляется с помощью констркуции цикла, в котором за каждую итерацию к сумме прибавляется очередная добавка, а затем вычисляется добавка для следующей итерации. Количество слагаемых в сумме определяется значением статического целочисленного поля N (значение поля равно 100). Поле описано со спецификатором уровня доступа private. Поэтому поле является закрытым и доступно только внутри кода класса MyMath. Поле Pi описано с идентификатором const. Это означает, что поле константное (его значение изменить нельзя). Константные поля автоматически реализуются как статические. Поэтому в главном методе программы доступ к этому полю получаем с помощью инструкции MyMath.Pi.

    Там (в главном методе) вычисляются значения для экспоненты и синуса. Для сравнения приведены контрольные значения, которые вычисляются с помощью статических методов Ехр() и Sin() класса Math. Несложно заметить, что совпадение более чем приемлемое.

Библиотечный класс Math (пространство имен System) содержит статические методы, через которые реализуются основные математические функции. Там также есть статические поля со значениями некоторых математических констант (основание натурального логарифма и число "пи").

    На следующем шаге мы рассмотрим ключевое слово this.

Предыдущий шаг Содержание Следующий шаг