На этом шаге мы рассмотрим следующий пример.

Значение цены игры v находится между -2 и 2.
Задача линейного программирования для игрока А
Максимизировать z = v
v - 3x1 + 2x2 + 5x3 ≤ 0,
v + x1 - 4x2 + 6x3 ≤ 0,
v + 3x1 + x2 - 2x3 ≤ 0,
x1 + x2 + x3 = 1,
x1, x2, x3 ≥ 0,
v не ограничена в знаке.
Оптимальным решением является x1 = 0,39, x2 = 0,31, x3 = 0,29 и v = -0,91.
Задача линейного программирования для игрока В
Минимизировать z = v
v - 3y1 + y2 + 3y3 ≥ 0,
v + 2y1 - 4y2 + y3 ≥ 0,
v + 5y1 + 6y2 - 2y3 ≥ 0,
y1 + y2 + y3 = 1,
y1, y2, y3 ≥ 0,
v не ограничена в знаке.
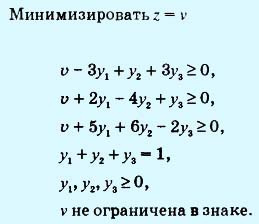
Оптимальным решением является y1 = 0,32, y2 = 0,08, y3 = 0,60 и v = -0,91.
На следующем шаге мы рассмотрим реализацию игр двух игроков с нулевой суммой в программе TORA.
