На этом шаге мы рассмотрим применение задачи инвестирования.
Предположим, вы хотите инвестировать 4000 долл. сейчас и 2000 долл. в начале каждого года, от второго до четвертого, считая от текущего года. Первый банк выплачивает годовой сложный процент 8% и премиальные на протяжении следующих четырех лет в размере 1,8, 1,7, 2,1 и 2,5% соответственно. Годовой сложный процент, предлагаемый вторым банком, на 0,2% ниже, чем предлагает первый банк, но его премиальные на 0,5% выше. Задача состоит в максимизации накопленного капитала к концу четвертого года.
Используя введенные выше обозначения, имеем следующее.

Этап 4.
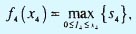
где
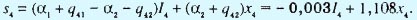
Функция s4 является линейной по I4 в области
0 ≤ I4 ≤
| . | Оптимальное решение | |
|---|---|---|
| Состояние | f4(x4) | I4 |
| x4 | 1,108x4 | 0 |
Этап 3.
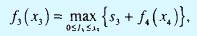
где
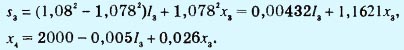
Cледовательно,
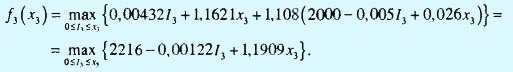
| . | Оптимальное решение | |
|---|---|---|
| Состояние | f3(x3) | I3 |
| x3 | 2216 + 1,909x3 | 0 |
Этап 2.
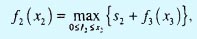
где
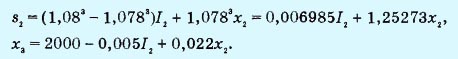
Cледовательно,
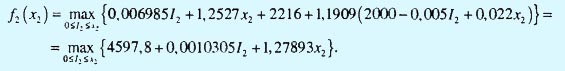
| . | Оптимальное решение | |
|---|---|---|
| Состояние | f2(x2) | I2 |
| x2 | 4597,8 + 1,27996x2 | x2 |
Этап 1.
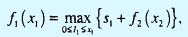
где

Cледовательно,

| . | Оптимальное решение | |
|---|---|---|
| Состояние | f1(x1) | I1 |
| x1 = 4000$ | 7157.7 + 1.38349x1 | 4000$ |
При вычислениях в обратном направлении получаем следующее.
х2 = 2000 - 0,005 * 4000 + 0,023 * 4000 = 2072 долл.,
х3 = 2000 - 0,005 * 2072 + 0,022 * 2072 = 2035,22 долл.,
х4 = 2000 - 0,005 * 0 + 0,026 * 2035,22 = 2052,92.
Следовательно, оптимальное решение будет записано следующим образом.
| Год | Оптимальное решение | Решение, принимаемое инвестором | Накопления |
|---|---|---|---|
| 1 | I1 = x1 | Инвестировать x1 = 4000 $ в первый банк | s1 = 5441,80 $ |
| 2 | I2 = x2 | Инвестировать x2 = 2072 $ в первый банк | s2 = 2610,13 $ |
| 3 | I3 = 0 | Инвестировать x3 = 2035,22 $ во второй банк | s3 = 2365,13 $ |
| 4 | I4 = 0 | Инвестировать x4 =2052,92 $ во второй банк | s4 = 2274,64 $ |
| Всего | 12 691,70 $ | ||
На следующем шаге рассмотрим решение задачи.
