На этом шаге мы рассмотрим применение метода графического решения задач линейного программирования для случая минимизации целевой функции.
Задача "диеты"
Фармацевтическая фирма ежедневно производит не менее 800 кг некой пищевой добавки, которая состоит из смеси кукурузной и соевой муки, состав которой представлен в следующей таблице.
| Мука | Белок, кг на кг муки | Клетчатка, кг на кг муки | Стоимость (руб./кг) |
|---|---|---|---|
| Кукурузная | 0,09 | 0,02 | 0,3 |
| Соевая | 0,6 | 0,06 | 0,9 |
Диетологи требуют, чтобы в пищевой добавке было не менее 30% белка и не более 5% клетчатки. Фирма хочет определить рецептуру смеси наименьшей стоимости с учетом требований диетологов.
Поскольку пищевая добавка состоит только из кукурузной и соевой муки, переменными для этой задачи, очевидно, будут x1 — количество (в кг) кукурузной муки, используемой в дневном производстве пищевой добавки; х2 — количество (в кг) соевой муки, используемой в дневном производстве пищевой добавки.
Целевая функция равна обшей стоимости пищевой добавки, производимой за один день, и должна быть минимальной. В данном случае это можно записать следующим образом:
Минимизировать z = 0,3 x1+ 0,9x2.
Ограничения модели должны отражать производственные требования и рекомендации диетологов. Фирма должна выпускать не менее 800 кг смеси в день.Соответствующее ограничение будет записано следующим образом: x1+ x2 ≥ 800.
Рассмотрим ограничение, связанное с количеством белка в пищевой добавке. Общее количество белка в смеси, состоящей из х1 кг кукурузной муки и х2 кг соевой муки, равно 0.09x1 + 0.6х2 (кг). Это количество должно составлять не менее 30% от общего объема смеси х1 + х2. Отсюда получаем следующее неравенство
0.09х1 + 0.6x2 ≥ 0.3(x1 + х2).
Аналогично строится ограничение для клетчатки:
0.02x1 + 0.06х2 ≤ 0.05(х1 + х2).
В последних двух неравенствах переменные x1 и х2 надо перенести из правых частей неравенств в левые. Окончательно модель примет следующий вид:
Минимизировать z = 0.3x1 + 0.9x2 при ограничениях
x1 + x2 ≥ 800,
0.21х1 - 0.3x2 ≤ 0,
0.03x1 - 0.01x2 ≥ 0,
x1, x2 ≥ 0.
На рис. 1 показано графическое решение этой задачи.
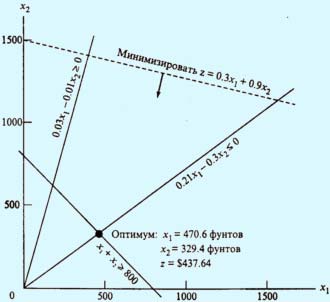
Рис. 1. Графическое решение задачи минимизации
Поскольку в данной модели следует минимизировать целевую функцию, поэтому нужно идти в направлении уменьшения ее значений (это направление на рис. 1 показано стрелкой). Оптимальное решение находится на пересечении прямых x1 + х2 = 800 и 0.21x1 - 0.30x2 = 0, откуда получаем х1 = 470.59 (кг) и х2 = 329.41 (кг). При этих значениях переменных минимальная стоимость производимой ежедневно пищевой добавки составляет z = 0.3 * 470.59 + 0.9 * 329.41 = 437.65 руб.
На следующем шаге рассмотрим понятие и применение дополнительных переменных в задачах линейного программирования.
