На этом шаге мы рассмотрим представление задачи линейного программирования в канонической форме.
Если математическая модель задачи линейного программирования имеет вид:
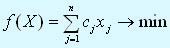
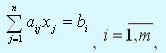
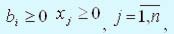
Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалента минимизации той же функции, взятой с противоположным знаком, и наоборот.
Правило приведения задачи линейного программирования к каноническому виду состоит в следующем:
- если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции;
- если в ограничениях правая часть отрицательна, то следует умножить это ограничение на -1;
- если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобразуются в равенства;
- если некоторая переменная xj не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными:
x3 = x3+ - x3-, где x3+, x3- ≥ 0.
Пример 1. Приведение к канонической форме задачи линейного программирования:
min L = 2x1 + x2 - x3;
2x2 - x3 ≤ 5;
x1 + x2 - x3 ≥ -1;
2x1 - x2 ≤ -3;
x1 ≤ 0; x2 ≥ 0; x3 ≥ 0.
Введем в каждое уравнение системы ограничений выравнивающие переменные x4, x5, x6. Система запишется в виде равенств, причем в первое и третье уравнения системы ограничений переменные x4, x6 вводятся в левую часть со знаком "+", а во второе уравнение переменная x5 вводится со знаком "-".
2x2 - x3 + x4 = 5;
x1 + x2 - x3 - x5 = -1;
2x1 - x2 + x6 = -3;
x4 ≥ 0; x5 ≥ 0; x6 ≥ 0.
Свободные члены в канонической форме должны быть положительными, для этого два последних уравнения умножим на -1:
2x2 - x3 + x4 = 5;
-x1 - x2 + x3 + x5 = 1;
-2x1 + x2 - x6 = 3.
В канонической форме записи задач линейного программирования все переменные, входящие в систему ограничений, должны быть отрицательными. Допустим, что x1 = x1' - x7, где x1' ≥ 0, x7 ≥ 0.
Подставляя данное выражение в систему ограничений и целевую функцию и, записывая переменные в порядке возрастания индекса, получим задачу линейного программирования, представленную в канонической форме:
Lmin = 2x1' + x2 - x3 - 2x7;
2x2 - x3 + x4 = 5;
-x1' - x2 + x3 + x5 + x7 = 1;
-2x1' + x2 - x6 + 2x7 = 3;
x1' ≥ 0; xi ≥ 0, i=2, 3, 4, 5, 6, 7.
На следующем шаге проведем графический анализ чувствительности задачи линейного программирования.
