Шаг 29.
Решение задач с помощью Tora (симплекс-метод)

    На этом шаге рассмотрим использование программы TORA для решения задачи линейного рпограммирования симплекс-методом.

    Используем задачу о компании "Русские краски" для рассмотрения деталей выполнения симплекс-метода в программе Tora.

1. Запустите Tora и откройте файл rm.or.
2. Выполните выбор Solve problem (Решить проблему) в меню Solve/Modify, затем в меню Procedure опцию User-guided procedure. В результате будет открыто окно с меню Algorithms (Выбор метода решения) (рис. 1)

   
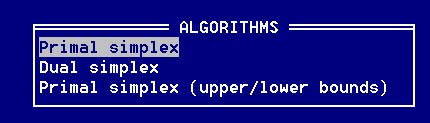
   Рис. 1. Окно с меню выбора метода решения

      Выберем прямой симплекс-метод (Primal simplex), в результате будет открыто подменю способа поиска первого базисного решения (меню Starting Solution) (рис. 2)

   
   Рис. 2. Подменю способа поиска базисного решения

       (Slack variables) позволяет строить первый базис из "переменных недостатка", выбираем этот пункт меню. Затем программа спрашивает, что делать дальше (меню Execution) рис. 3:

   
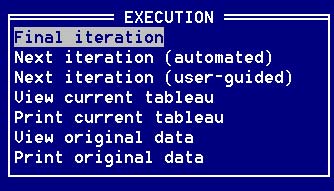
   Рис. 3. Меню Execution

   • решить задачу (Final iteration),
   • выполнить одну (очередную) итерацию (Next iteration) автоматически или под управлением пользователя,
   • просмотреть или распечатать текущую симплекс-таблицу (current tableau),
   • просмотреть или распечатать исходные данные (original data).

       Посмотрим первую симплекс-таблицу (View current tableau) рис. 4.

   
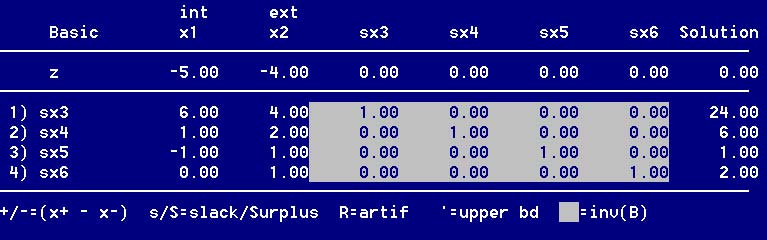
   Рис. 4. Первая симплекс-таблица

       Нижние четыре строки этой таблицы представляют равенства ограничений; значения правых частей этих равенств даны в столбце "Решение" (Solution).

3. Нажмите F5 для перехода к меню Execution.
4. Выберите опцию Next iteration (automated) и просмотрите новую таблицу (View current tableau). В результате будет отображена новая таблица для второй итерации (рис. 5) сравните полученные результаты с предыдущим шагом.

   
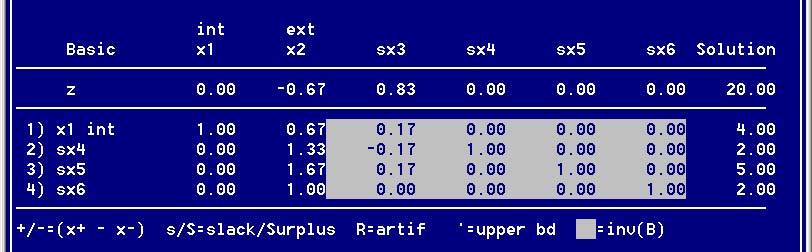
   Рис. 5. Вторая итерация

5. Нажмите F5 для перехода к меню Execution.
6. Рассмотрим еще один способ выбора включаемых и исключаемых переменных. Выберите опцию Next iteration (uses-guided). В открывшемся подменю (select ENTERING var) выберите Users choice. Далее следует ввести номер включаемой переменной (нужно ввести цифру 2, т.к. вводим переменную х₂, а она в списке вторая). Нажимаем Enter и вводим номер исключаемой переменной (цифра 4, т.к. исключаем sx₄, которая в списке занимает четвертое место). Просмотрите новую таблицу (View current tableau). В результате будет отображена новая таблица для третьей итерации (рис. 6).

   
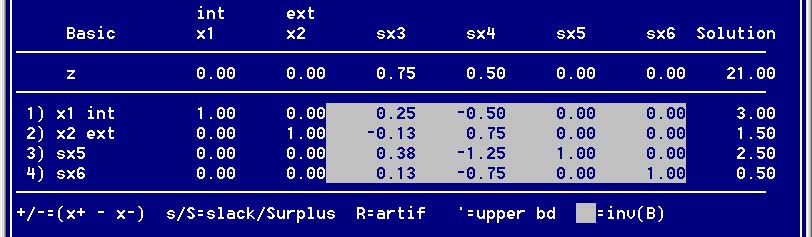
   Рис. 6. Третья итерация

       Поскольку z-строка не имеет отрицательных коэффициентов, соответствующих небазисным переменным sx₃ и sx₄, полученное решение оптимально.

       Оптимальное решение задачи линейного программирования можно "считать" из симплекс-таблицы следующим образом. Неотрицательные (базисные) переменные представлены в столбце "Базис", а их значения — в столбце "Решение". В данном примере имеем следующее:

   • ежедневно следует производить 3 т краски для наружных работ;
   • ежедневно следует производить 1,5 т краски для внутренних работ;
   • ежедневный доход составляет 21000 д.е.

    На следующем шаге рассмотрим решение нескольких задач.

Предыдущий шаг Содержание Следующий шаг