На этом шаге мы рассмотрим правила передачи аргументов в функцию и рекурсивные функции.
В JavaScript действуют следующие правила передачи аргументов функции:
- аргументы примитивных типов передаются функции по значению. Иными словами, формальным аргументам присваиваются значения фактических аргументов на момент вызова и, если даже операторы в теле функции изменят значение какого-либо аргумента, то это изменение не коснется переменной, чье значение передавалось в качестве аргумента;
- объекты (и встроенные, и определенные пользователем) передаются по ссылке. Это означает, что все изменения свойств объекта в теле функции производятся непосредственно в самом объекте, а не в его локальной копии и, следовательно, сохраняются после возврата из функции.
Важной особенностью языка JavaScript является то, что функция может вызывать не только другие функции, но и сама себя. Такие функции называются рекурсивными. Во многих случаях использование рекурсии позволяет писать краткий код вместо сложных вложенных циклов. Следует, однако, учитывать, что рекурсия работает медленнее, чем обычный цикл, и пользоваться ей только в тех случаях, когда это действительно оправдано.
Приведем пример функции, вычисляющей факториал числа (факториал числа n равен 1 * 2 * ... * n):
<HTML> <HEAD> <TITLE>Рекурсивные функции</TITLE> <SCRIPT LANGUAGE="JavaScript"> <!-- function factorial (n) { return (n<=1)?1:n * factorial(n-1); } var x = 5; var y = factorial (x); alert ("Факториал числа "+x+" равен "+y); //--> </SCRIPT> </HEAD> <BODY> </BODY> </HTML>
Результат работы скрипта приведен на рисунке 1.
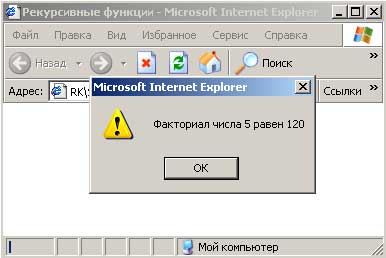
Рис.1. Использование рекурсивной функции
Неаккуратно написанная рекурсивная функция может войти в бесконечный цикл и никогда не вернуть результата. Поэтому при использовании рекурсии всегда нужно предусмотреть точку выхода из рекурсии. Такой точкой выхода является здесь проверка условия n<=1. Как только это условие будет выполнено, функция вернет значение 1, а до этого момента значение функции будет равно n*factorial(n-1):
5 * factorial (4);
5 * 4 * factorial (3);
5 * 4 * 3 * factorial (2);
. . . . .
5 * 4 * 3 * 2 * 1. //"Сработало" условие выхода.
На следующем шаге мы рассмотрим вопросы, связанные с областью видимости переменных.
