На этом шаге мы рассмотрим алгоритмы создаени бинарных деревьев поиска и приведем библиотеку функций для работы с бинарными деревьями.
Для представления бинарных деревьев воспользуемся двумя способами, каждый из которых основан на определенном списочном представлении дерева.
Первый способ.
Бинарное дерево поиска состоит из узлов вида:
(Корень (Левое-поддерево Правое-поддерево))
В каждом узле выполнено следующее условие: все элементы из узлов его левого поддерева в некотором упорядочении (например, по числовой величине или в алфавитном порядке) предшествуют элементу из узла и соответственно элементы из узлов правого поддерева следуют за ними.
Пример 1.
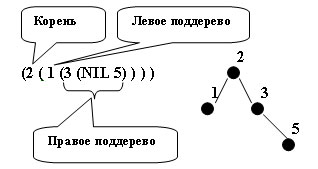
Рис.1. Пример 1
Пример 2.
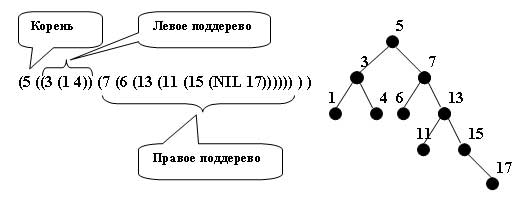
Рис.2. Пример 2
Заметим, что если TREE имеет представление вида
(Корень (Левое-поддерево Правое-поддерево)) ,
( Корень (Левое-поддерево Правое-поддерево) )
------ --------------- ----------------
^ ^ ^
¦ ¦ ¦
(CAR TREE) (CAR (CADR TREE)) (CADR (CADR TREE))
Второй способ [1].
Бинарное дерево поиска состоит из узлов вида:
(Элемент Левое-поддерево Правое-поддерево)
В каждом узле выполнено следующее условие: все элементы из узлов его левого поддерева в некотором упорядочении (например, по числовой величине или в алфавитном порядке) предшествуют элементу из узла и соответственно элементы из узлов правого поддерева следуют за ними.
Пример 3.
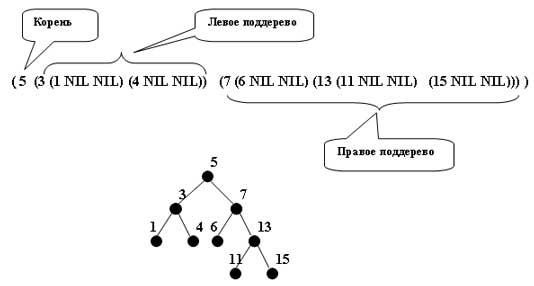
Рис.3. Пример 3
Заметим, что если TREE имеет представление вида
(Корень Левое-поддерево Правое-поддерево)
( Корень Левое-поддерево Правое-поддерево )
------ --------------- ----------------
^ ^ ^
¦ ¦ ¦
(CAR TREE) (CADR TREE) (CADDR TREE)
Пример 4. Библиотека для работы с бинарными деревьями.
(DEFUN TEST (LAMBDA NIL
(PRINT "Построим дерево со счетчиком повторяющихся элементов!")
(SETQ TREE NIL)
(LOOP
(PRINT "Введите очередной элемент дерева:")
(SETQ A (READ)) ( (EQ A '!) )
(PRINT (SETQ TREE (ADDTREE1 A TREE)))
(PRINT "---------------------------")
)
(PRINT "----------------------------------")
(PRINT "Построение дерева: ") (SETQ TREE NIL)
(LOOP
(PRINT "Введите очередной элемент дерева:")
(SETQ A (READ)) ( (EQ A '!) )
(PRINT (SETQ TREE (ADDTREE A TREE)))
)
(PRINT "-----------------------------")
(PRIN1 "Корень дерева: ")
(PRINT (ROOT TREE))
(PRIN1 "Левое поддерево: ")
(PRINT (LEFT TREE))
(PRIN1 "Правое поддерево: ")
(PRINT (RIGHT TREE))
(PRIN1 "Обход дерева в ширину: ")
(PRINT (REMBER
NIL
(LISTATOMS (UNTREE (TOP TREE) TREE))))
(PRIN1 "Левосторонний обход дерева: ")
(PRINT (UNTREE1 TREE))
(PRIN1 "Число уровней в дереве: ")
(PRINT (TOP TREE))
(PRIN1 "Количество листьев в дереве: ")
(PRINT (NLIST TREE))
(PRIN1 "Копия дерева: ")
(PRINT (TCOPY TREE))
(PRINT "-----------------------------")
(PRINT "Приступим к поиску элемента в дереве!")
(LOOP
(PRINT "Введите искомый элемент дерева:")
(SETQ A (READ))
( (EQ A '!) )
(PRINT (SEARCH A TREE))
)
(PRINT "------------------------------")
(PRINT "Приступим к удалению элемента!")
(LOOP
(PRINT "Введите удаляемый элемент дерева:")
(SETQ A (READ))
( (EQ A '!) )
(PRINT (SETQ TREE (DELETE A TREE)))
)
(PRINT "------------------------------")
(PRINT "Приступим к удалению элемента другим способом!")
(LOOP
(PRINT "Введите удаляемый элемент дерева:")
(SETQ A (READ))
( (EQ A '!) )
(PRINT (SETQ TREE (DELETE1 A TREE)))
)
(PRINT "----------------------------------")
(PRINT "Приступим к выделению поддеревьев!")
(LOOP
(PRINT "Введите какой-либо элемент дерева:")
(SETQ A (READ))
( (EQ A '!) 'END )
(PRINT (PRETREE A TREE))
(PRINT (POSTTREE A TREE))
(PRINT (UNITETREE (PRETREE A TREE)
(POSTTREE A TREE)))
(PRINT "---------------------------")
)
))
; ------------------------------
(DEFUN ADDTREE1 (LAMBDA (A TREE)
; Функция ADDTREE добавляет в дерево поиска TREE элемент A
; с подсчетом количества поторений элемента A при вводе
(COND ( (NULL TREE) (LIST (CONS A 0) NIL NIL) )
( (EQUAL A (CAAR TREE))
(LIST (CONS A (+ (CDAR TREE) 1))
(CADR TREE) (CADDR TREE)) )
( (< A (CAAR TREE))
(LIST (CAR TREE) (ADDTREE1 A (CADR TREE))
(CADDR TREE)) )
( T (LIST (CAR TREE)
(CADR TREE) (ADDTREE1 A (CADDR TREE))) )
)
))
; -----------------------------
(DEFUN ADDTREE (LAMBDA (A TREE)
; Функция ADDTREE добавляет в дерево поиска TREE элемент A
(COND ( (NULL TREE) (LIST A NIL NIL) )
( (EQUAL A (CAR TREE)) TREE )
( (< A (CAR TREE))
(LIST (CAR TREE) (ADDTREE A (CADR TREE))
(CADDR TREE)) )
( T (LIST (CAR TREE) (CADR TREE)
(ADDTREE A (CADDR TREE))) )
)
))
; -------------------------
(DEFUN CONSTR (LAMBDA (LST)
; Функция CONSTR строит дерево из списка LST в обратном порядке
(COND ( (NULL LST) NIL )
( T (ADDTREE (CAR LST) (CONSTR (CDR LST))) )
)
))
; ---------------------------
(DEFUN CONSTREE (LAMBDA (LST)
; Функция CONSTR строит дерево из списка LST в прямом порядке
(CONSTR (REVERSE LST))
))
; ----------------------------
(DEFUN SEARCH (LAMBDA (A TREE)
; Функция SEARCH ищет в дереве TREE элемент A.
; В случае успеха функция возвращает поддерево дерева
; TREE, в котором элемент A является корнем; в случае
; неудачного поиска функция возвращает NIL
(COND ( (NULL TREE) NIL )
( (EQUAL A (CAR TREE)) TREE )
( (< A (CAR TREE)) (SEARCH A (CADR TREE)) )
( T (SEARCH A (CADDR TREE)) )
)
))
; ----------------------------------
(DEFUN REPLACE (LAMBDA (OLD NEW LST)
; Замена в списке LST подсписка OLD на подсписок NEW
(COND ( (ATOM LST) LST )
( (EQUAL OLD LST) NEW )
( T (CONS (REPLACE OLD NEW (CAR LST))
(REPLACE OLD NEW (CDR LST))) )
)
))
; ------------------------
(DEFUN ROOT (LAMBDA (TREE)
; Функция ROOT возвращает корень дерева TREE
(CAR TREE)
))
; ------------------------
(DEFUN LEFT (LAMBDA (TREE)
; Функция возвращает левое поддерево дерева TREE
(CADR TREE)
))
; -------------------------
(DEFUN RIGHT (LAMBDA (TREE)
; Функция возвращает правое поддерево дерева TREE
(CADDR TREE)
))
; -----------------------------
(DEFUN RIGHTLIST (LAMBDA (TREE)
; Возвращает самый правый лист дерева TREE
(COND ( (NULL (RIGHT TREE)) (CAR TREE) )
( T (RIGHTLIST (RIGHT TREE)) )
)
))
; ----------------------------
(DEFUN LEFTLIST (LAMBDA (TREE)
; Возвращает самый левый лист дерева TREE
(COND ( (NULL (LEFT TREE)) (CAR TREE) )
( T (LEFTLIST (LEFT TREE)) )
)
))
; ------------------------------
(DEFUN DELETE (LAMBDA (ATM TREE)
; Удаление узла ATM из дерева TREE
; (нерекурсивный вариант удаления)
(SETQ SUBTREE (SEARCH ATM TREE))
(COND ( (NULL SUBTREE) (PRINT "Узла в дереве нет!") )
( T
; Узел ATM в дереве TREE найден
(COND ( (EQUAL SUBTREE (LIST ATM NIL NIL))
; Найденный узел - лист
(REPLACE SUBTREE NIL TREE)
)
( (AND (NOT (NULL (LEFT SUBTREE)))
(NOT (NULL (RIGHT SUBTREE))))
; Найденный узел имеют оба поддерева
(SETQ UZEL
(RIGHTLIST (LEFT SUBTREE)))
(RPLACA SUBTREE UZEL)
(COND ( (NULL (RIGHT
(LEFT SUBTREE)))
(REPLACE (LEFT SUBTREE)
(CADR (LEFT SUBTREE))
TREE) )
( (NULL (LEFT
(LEFT SUBTREE)))
(REPLACE (LEFT SUBTREE)
(CADDR (LEFT SUBTREE))
TREE) )
( T (REPLACE (LIST UZEL
NIL NIL)
NIL TREE) )
)
)
( (NULL (RIGHT SUBTREE))
; У найденного узла - только левое поддерево
(REPLACE SUBTREE (CADR SUBTREE)
TREE)
)
( (NULL (LEFT SUBTREE))
; У найденного узла - только правое поддерево
(REPLACE SUBTREE (CADDR SUBTREE)
TREE)
)
)
)
)
))
; -------------------------------
(DEFUN DELETE1 (LAMBDA (ATM TREE)
; Удаление узла ATM из дерева TREE
; (рекурсивный вариант удаления)
(COND ( (NULL TREE) NIL )
( (< ATM (ROOT TREE))
(LIST (CAR TREE)
(DELETE1 ATM (LEFT TREE))
(RIGHT TREE))
)
( (> ATM (ROOT TREE))
(LIST (CAR TREE)
(LEFT TREE)
(DELETE1 ATM (RIGHT TREE)))
)
( T (COND ( (NULL (RIGHT TREE)) (LEFT TREE) )
( (NULL (LEFT TREE)) (RIGHT TREE) )
( T (LIST (UD (LEFT TREE))
(DELETE1
(UD (LEFT TREE))
(LEFT TREE))
(RIGHT TREE)) )) )
)
))
; ----------------------
(DEFUN UD (LAMBDA (TREE)
; Вспомогательныя функция для функции DELETE1
(COND ( (NULL (RIGHT TREE)) (CAR TREE) )
( T (UD (RIGHT TREE)) )
)
))
; -----------------------
(DEFUN TOP (LAMBDA (TREE)
; Функция TOP возвращает число уровней в дереве TREE
; (корень дерева расположен на нулевом уровне)
(COND ( (NULL TREE) -1 )
( T (+ 1 (MAX (TOP (LEFT TREE))
(TOP (RIGHT TREE)))) )
)
))
; ----------------------
(DEFUN MAX (LAMBDA (M N)
; Функция MAX возвращает большее из чисел M и N
(COND ( (> M N) M )
( T N )
)
))
; -------------------------
(DEFUN NLIST (LAMBDA (TREE)
; Функция NLIST возвращает количество листьев дерева TREE
(COND ( (NULL TREE) 0 )
( (EQUAL (CDR TREE) (LIST NIL NIL)) 1 )
( T (+ (NLIST (LEFT TREE)) (NLIST (RIGHT TREE))) )
)
))
; -------------------------
(DEFUN TCOPY (LAMBDA (TREE)
; Функция TCOPY возвращает копию дерева TREE
(COND ( (ATOM TREE) TREE )
( T (CONS (TCOPY (CAR TREE))
(TCOPY (CDR TREE))) )
)
))
; -----------------------------
(DEFUN PRETREE (LAMBDA (A TREE)
; Функция PRETREE выделяет в отдельное дерево из дерева
; TREE все узлы, предшествующие данному элементу A
(COND ( (NULL TREE) NIL )
( (< (CAR TREE) A)
(LIST (CAR TREE) (CADR TREE)
(PRETREE A (CADDR TREE))) )
( T (PRETREE A (CADR TREE)) )
)
))
; ------------------------------
(DEFUN POSTTREE (LAMBDA (A TREE)
; Функция POSTTREE выделяет в отдельное дерево из дерева
; TREE все узлы, следующие за данным элементом A
(COND ( (NULL TREE) NIL )
( (< (CAR TREE) A)
(POSTTREE A (CADDR TREE)) )
( T (LIST (CAR TREE)
(POSTTREE A (CADR TREE))
(CADDR TREE)) )
)
))
; ------------------------------------
(DEFUN UNITETREE (LAMBDA (TREE1 TREE2)
; Функция UNITETREE объединяет два дерева поиска
; TREE1 и TREE2 в одно дерево поиска
(COND ( (NULL TREE1) TREE2 )
( (NULL TREE2) TREE1 )
( T (LIST (CAR TREE1)
(UNITETREE (PRETREE (CAR TREE1)
TREE2)
(CADR TREE1))
(UNITETREE (POSTTREE (CAR TREE1)
TREE2)
(CADDR TREE1))) ) )
))
; ----------------------------
(DEFUN UNTREE (LAMBDA (M TREE)
; "Грязный" обход дерева TREE в "ширину", начиная
; с 0-го уровня и кончая M-м уровнем
(COND ( (EQ M 0) (CAR TREE) )
( T (LIST (UNTREE (- M 1) TREE)
(SEE M TREE)) )
)
))
; ---------------------------
(DEFUN UNTREE1 (LAMBDA (TREE)
; Левосторонний обход дерева TREE
(REMBER NIL (LISTATOMS TREE))
))
; -------------------------
(DEFUN SEE (LAMBDA (N TREE)
; Обход дерева TREE в "ширину" и создание "грязного"
; списка, содержащего вершины N-го уровня дерева
(COND ( (EQ N 0) (CAR TREE) )
( (EQ N 1)
(LIST (CAR (CADR TREE)) (CAR (CADDR TREE)))
)
( T (LIST (SEE (- N 1) (CADR TREE))
(SEE (- N 1) (CADDR TREE))) )
)
))
; -----------------------------
(DEFUN LISTATOMS (LAMBDA (TREE)
; Функция LISTATOMS возвращает список, составленный из
; элементов (включая NIL !), входящих в дерево поиска TREE
(COND ( (NULL TREE) NIL)
( (ATOM (CAR TREE))
(CONS (CAR TREE) (LISTATOMS (CDR TREE))) )
( T (APPEND (LISTATOMS (CAR TREE))
(LISTATOMS (CDR TREE))) )
)
))
; -----------------------------
(DEFUN REMBER (LAMBDA (ATM LST)
; Функция REMBER возвращает список, в котором удалены
; все вхождения элемента ATM в список LST
(COND ( (NULL LST) NIL )
( (EQ ATM (CAR LST)) (REMBER ATM (CDR LST)) )
( T (CONS (CAR LST) (REMBER ATM (CDR LST))) )
)
))
; -------------------------------
(DEFUN APPEND (LAMBDA (LST1 LST2)
; Функция APPEND возвращает список, состоящий из
; элементов списка LST1, добавленных к списку LST2
(COND ( (NULL LST1) LST2 )
( (NULL LST2) LST1 )
( T (CONS (CAR LST1)
(APPEND (CDR LST1) LST2)) )
)
))
Замечание. Функции DELETE1 и UD "дословно" переписаны со следующей рекурсивной процедуры, написанной Н.Виртом [2]:
PROCEDURE U_d_a_l_d_r (var d: Ref; k: Integer); {Удаление узла с ключом k из деpева d. } { Ref - тип указатель на узел дерева } var q: Ref; { -------------------------- } PROCEDURE U_d (var r: Ref); BEGIN If r^.Right=Nil then begin q^.Key := r^.Key; q^.Count := r^.Count; q := r; r := r^.Left; { Исключили узел... } Dispose (q) { Освободили память } end else U_d (r^.Right) END; { ----- } BEGIN If d=Nil then { Пеpвый случай алгоpитма удаления } Writeln ('Узел с заданным ключом в деpеве не найден...') else { 1Поиск узла с заданным ключом 0 } If k<d^.Key then U_d_a_l_d_r (d^.Left,k) else If k>d^.Key then U_d_a_l_d_r (d^.Right,k) else begin { Узел найден, необходимо его удалить } { Втоpой случай алгоpитма удаления } q := d; If q^.Right = Nil then d := q^.Left else If q^.Left=Nil then d := q^.Right else { Тpетий случай } { алгоpитма удаления } U_d (q^.Left) end END;
(1)Хювенен Э., Сеппянен Й. Мир Лиспа. В 2-х т. Т.1: Введение в язык Лисп и функциональное программирование. - М.: Мир, 1990. - 447 с.
(2)Вирт Н. Алгоритмы + структуры данных = программы. -М.: Мир, 1985. - 406 с.
На следующем шаге мы познакомимся с TRIE-структурами.
