На этом шаге мы рассмотрим использование метода наименьщих квадратов и оценим его эффективность.

    Линейная регрессия или обычный метод наименьших квадратов (ordinary least squares, OLS) - это самый простой и наиболее традиционный метод регрессии. Линейная регрессия находит параметры w и b, которые минимизируют среднеквадратическую ошибку (mean squared error) между спрогнозированными и фактическими ответами у в обучающем наборе. Среднеквадратичная ошибка равна сумме квадратов разностей между спрогнозированными и фактическими значениями. Линейная регрессия проста, что является преимуществом, но в то же время у нее нет инструментов, позволяющих контролировать сложность модели.

    Ниже приводится программный код, который строит модель, приведенную на рисунке 1 предыдущего шага:

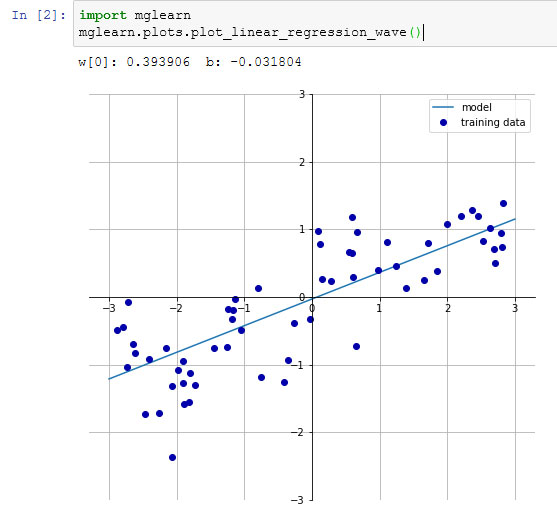
Рис.1. Рисунок 1 предыдущего шага с прогнозом линейной модели для набора данных wave

[In 6]:
import mglearn
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X, y = mglearn.datasets.make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
lr = LinearRegression().fit(X_train, y_train)

    Параметры "наклона" (w), также называемые весами или коэффициентами (coefficients), хранятся в атрибуте coef_, тогда как сдвиг (offset) или константа (intercept), обозначаемая как b, хранится в атрибуте intercept_:

[In 8]:
print("lr.coef_: {}".format(lr.coef_))
print("lr.intercept_: {}".format(lr.intercept_)) 

lr.coef_: [0.39390555]
lr.intercept_: -0.031804343026759746

Вы можете заметить странный символ подчеркивания в конце названий атрибутов coef_ и intercept_. Библиотека scikit-learn всегда хранит все, что является производным от обучающих данных, в атрибутах, которые заканчиваются символом подчеркивания. Это делается для того, чтобы не спутать их с пользовательскими параметрами.

    Атрибут intercept_ - это всегда отдельное число с плавающей точкой, тогда как атрибут coef_ - это массив NumPy, в котором каждому элементу соответствует входной признак. Поскольку в наборе данных wave используется только один входной признак, lr.coef_ содержит только один элемент.

    Давайте посмотрим правильность модели на обучающем и тестовом наборах:

[In 11]:
print("Правильность на обучающем наборе: {:.2f}".format(lr.score(X_train, y_train)))
print("Правильность на тестовом наборе: {:.2f}".format(lr.score(X_test, y_test)))

Правильность на обучающем наборе: 0.67
Правильность на тестовом наборе: 0.66

    Значение R² в районе 0.66 указывает на не очень хорошее качество модели, однако можно увидеть, что результаты на обучающем и тестовом наборах очень схожи между собой. Возможно, это указывает на недообучение, а не переобучение. Для этого одномерного массива данных опасность переобучения невелика, поскольку модель очень проста (или строга). Однако для высокоразмерных наборов данных (наборов данных с большим количеством признаков) линейные модели становятся более сложными и существует более высокая вероятность переобучения. Давайте посмотрим, как LinearRegression сработает на более сложном наборе данных, например, на наборе Boston Housing. Вспомним, что этот набор данных имеет 506 примеров (наблюдений) и 105 производных признаков. Во-первых, мы загрузим набор данных и разобьем его на обучающий и тестовый наборы. Затем построим модель линейной регрессии:

[In 13]:
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)

    При сравнении правильности на обучающем и тестовом наборах выясняется, что мы очень точно предсказываем на обучающем наборе, однако R² на тестовом наборе имеет довольно низкое значение:

[In 15]:
print("Правильность на обучающем наборе: {:.2f}".format(lr.score(X_train, y_train))) 
print("Правильность на тестовом наборе: {:.2f}".format(lr.score(X_test, y_test)))

Правильность на обучающем наборе: 0.95
Правильность на тестовом наборе: 0.61

    Это несоответствие между правильностью на обучающем наборе и правильностью на тестовом наборе является явным признаком переобучения и поэтому мы должны попытаться найти модель, которая позволит нам контролировать сложность. Одна из наиболее часто используемых альтернатив стандартной линейной регрессии - гребневая регрессия, которую мы рассмотрим на следующем шаге.

    На следующем шаге мы рассмотрим гребневую регрессию.

Предыдущий шаг Содержание Следующий шаг