На этом шаге мы проведем анализ результатов, полученных при использовании случайного леса.

    Давайте применим случайный лес, состоящий из пяти деревьев, к набору данных two_moons, который мы изучали ранее:

[In 2]:
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier 
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, 
                                                    random_state=42)
forest = RandomForestClassifier(n_estimators=5, random_state=2)
forest.fit(X_train, y_train)

    Деревья, которые строятся в рамках случайного леса, сохраняются в атрибуте estimator_. Давайте визуализируем границы принятия решений, полученные каждым деревом, а затем выведем агрегированный прогноз, выданный лесом (рисунок 1):

[In 3]:
fig, axes = plt.subplots(2, 3, figsize=(20, 10))
for i, (ax, tree) in enumerate(zip(axes.ravel(), forest.estimators_)): 
    ax.set_title("Дерево {}".format(i))
    mglearn.plots.plot_tree_partition(X_train, y_train, tree, ax=ax)

mglearn.plots.plot_2d_separator(forest, X_train, fill=True, ax=axes[-1, -1], 
                                alpha=.4)
axes[-1, -1].set_title("Случайный лес")
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)

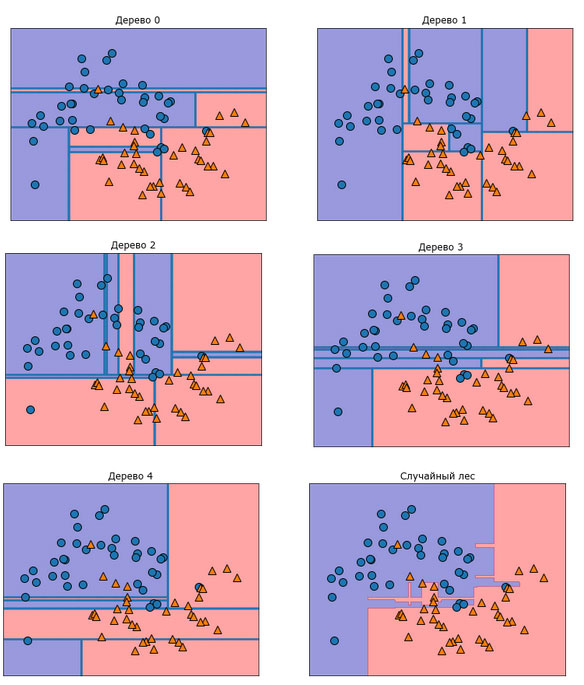
Рис.1. Границы принятия решений, найденные пятью рандомизированными деревьями решений, и граница принятия решений, полученная путем усреднения их спрогнозированных вероятностей

    На рисунках отчетливо видно, что границы принятия решений, полученные с помощью пяти деревьев, существенно различаются между собой. Каждое дерево совершает ряд ошибок, поскольку из-за бутстрепа некоторые точки исходного обучающего набора фактически не были включены в обучающие наборы, по которым строились деревья.

    В отличие от отдельных деревьев случайный лес переобучается в меньшей степени и дает гораздо более чувствительную (гибкую) границу принятия решений. В реальных примерах используется гораздо большее количество деревьев (часто сотни или тысячи), что приводит к получению еще более чувствительной границы.

    В качестве еще одного примера давайте построим случайный лес, состоящий из 100 деревьев, на наборе данных Breast Cancer:

[In 4]:
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, 
                                                    cancer.target, random_state=0) 
forest = RandomForestClassifier(n_estimators=100, random_state=0)
forest.fit(X_train, y_train)
print("Правильность на обучающем наборе: {:.3f}".
      format(forest.score(X_train, y_train))) 
print("Правильность на тестовом наборе: {:.3f}".
      format(forest.score(X_test, y_test)))

Правильность на обучающем наборе: 1.000
Правильность на тестовом наборе: 0.972

    Без настройки каких-либо параметров случайный лес дает нам правильность 97%, это лучше результата линейных моделей или одиночного дерева решений. Мы могли бы отрегулировать настройку max_features или применить предварительную обрезку, как это делали для одиночного дерева решений. Однако часто параметры случайного леса, выставленные по умолчанию, работают уже сами по себе достаточно хорошо.

    Как и дерево решений, случайный лес позволят вычислить важности признаков, которые рассчитываются путем агрегирования значений важности по всем деревьям леса. Как правило, важности признаков, вычисленные случайным лесом, являются более надежным показателем, чем важности, вычисленные одним деревом. Посмотрите на рисунок 2.

[In 5]:
def plot_feature_importances_cancer(model): 
    n_features = cancer.data.shape[1]
    plt.barh(range(n_features), model.feature_importances_, align='center') 
    plt.yticks(np.arange(n_features), cancer.feature_names) 
    plt.xlabel("Важность признака") 
    plt.ylabel("Признак") 

plot_feature_importances_cancer(forest)

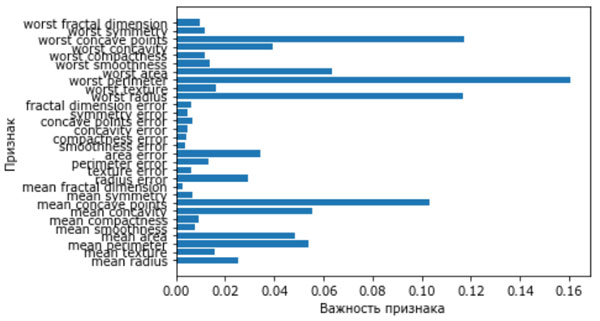
Рис.2. Важности признаков, вычисленные случайным лесом для набора данных Breast Cancer

    На рисунке видно, что в отличие от одиночного дерева решения случайный лес вычисляет ненулевые значения важностей для гораздо большего числа признаков. Как и дерево решений, случайный лес также присваивает высокое значение важности признаку "worst radius", однако в качестве наиболее информативного признака выбирает "worst perimeter". Случайность, лежащая в основе случайного леса, заставляет алгоритм рассматривать множество возможных интерпретаций. Это приводит к тому, что случайный лес дает гораздо более широкую картину данных, чем одиночное дерево.

    На следующем шаге мы рассмотрим преимущества, недостатки и параметры.

Предыдущий шаг Содержание Следующий шаг