На этом шаге мы рассмотрим реализацию такого прогнозирования.
Вывод метода predict_proba - это вероятность каждого класса и часто его легче понять, чем вывод метода decision_function. Для бинарной классификации он всегда имеет форму (n_samples, 2):
[In 9]: print("Форма вероятностей: {}".format(gbrt.predict_proba(X_test).shape)) Форма вероятностей: (25, 2)
Первый элемент строки - это оценка вероятности первого класса, а второй элемент строки - это оценка вероятности второго класса. Поскольку речь идет о вероятности, то значения в выводе predict_proba всегда находятся в диапазоне между 0 и 1, а сумма значений для обоих классов всегда равна 1:
# выведем первые несколько элементов predict_proba [In 10]: print("Спрогнозированные вероятности:\n{}".format( gbrt.predict_proba(X_test[:6]))) Спрогнозированные вероятности: [[0.01573626 0.98426374] [0.84575653 0.15424347] [0.98112869 0.01887131] [0.97407033 0.02592967] [0.01352142 0.98647858] [0.02504637 0.97495363]]
Поскольку вероятности обоих классов в сумме дают 1, один из классов всегда будет иметь определенность, превышающую 50%. Этот класс и будет спрогнозирован.
Поскольку вероятности - это числа с плавающей точкой, то маловероятно, что они обе будут точно равны 0.500. Однако, если это произойдет, то прогноз будет осуществлен случайным образом.
В предыдущем выводе видно, что большинство точек отнесены к тому или иному классу с высокой долей определенности. Соответствие спрогнозированной неопределенности фактической зависит от модели и параметров. Для переобученной модели характерна высокая доля определенности прогнозов, даже если они и ошибочные. Модель с меньшей сложностью обычно характеризуется высокой долей неопределенности своих прогнозов. Модель называется калиброванной (calibrated), если вычисленная неопределенность соответствует фактической: в калиброванной модели прогноз, полученный с 70%-ной определенностью, будет правильным в 70% случаев.
В следующем примере (рисунок 1) мы снова покажем границу принятия решения для набора данных, а также вероятности для класса 1:
[In 11]: fig, axes = plt.subplots(1, 2, figsize=(13, 5)) mglearn.tools.plot_2d_separator( gbrt, X, ax=axes[0], alpha=.4, fill=True, cm=mglearn.cm2) scores_image = mglearn.tools.plot_2d_scores( gbrt, X, ax=axes[1], alpha=.5, cm=mglearn.ReBl, function='predict_proba') for ax in axes: # размещаем на графике точки обучающего и тестового наборов mglearn.discrete_scatter(X_test[:, 0], X_test[:, 1], y_test, markers='^', ax=ax) mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train, markers='o', ax=ax) ax.set_xlabel("Характеристика 0") ax.set_ylabel("Характеристика 1") cbar = plt.colorbar(scores_image, ax=axes.tolist()) axes[0].legend(["Тест класс 0", "Тест класс 1", "Обуч класс 0", "Обуч класс 1"], ncol=4, loc=(.1, 1.1))
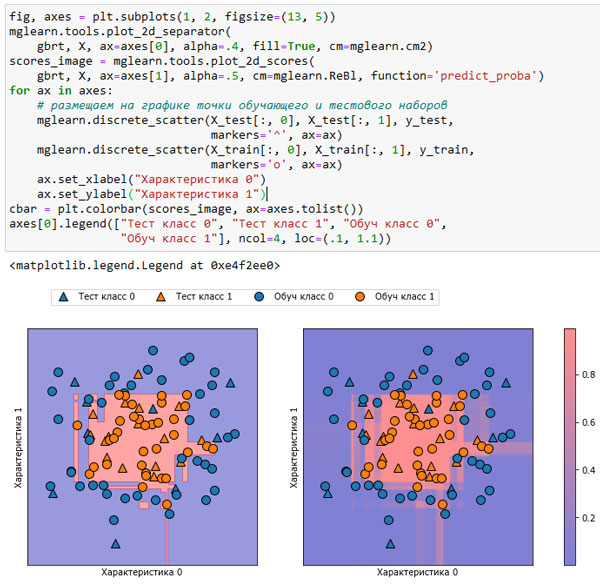
Рис.1. Граница принятия решений (слева) спрогнозированные вероятности для модели градиентного бустинга, показанной на рисунке 1 75 шага
Границы на этом рисунке определены гораздо более четко, а небольшие участки неопределенности отчетливо видны.
На сайте scikit-learn дается сравнение различных моделей и визуализации оценок неопределенности для этих моделей. Мы воспроизвели их на рисунке 2 и рекомендуем ознакомиться с ними.
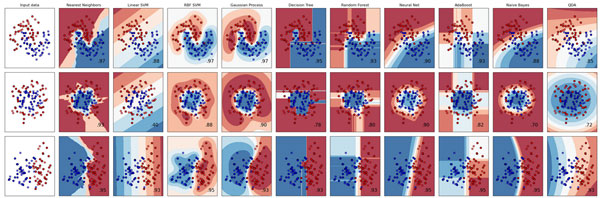
Рис.2. Сравнение нескольких классификаторов scikit-learn, построенных на синтетических наборах данных (изображение взято с сайта http://scikit-learn.org)
На следующем шаге мы рассмотрим неопределенность в мультиклассовой классификации.
