На этом шаге мы приведем алгоритм нахождения этих параметров.

    С помощью конвейеров мы можем инкапсулировать все этапы предварительной обработки в одной модели scikit-learn. Еще одно преимущество конвейеров заключается в том, что теперь мы можем настроить параметры предварительной обработки, используя результат, полученный с помощью модели контролируемого машинного обучения (то есть результат решения регрессионной или классификационной задачи). При работе с набором данных boston мы перед применением гребневой регрессии создали полиномиальные признаки. Теперь давайте используем конвейер. Конвейер включает три этапа - масштабирование данных, вычисление полиномиальных признаков и построение гребневой регрессии:

[In 28]:
from sklearn.datasets import load_boston
boston = load_boston()
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target,
                                                    random_state=0)

from sklearn.preprocessing import PolynomialFeatures
pipe = make_pipeline(
    StandardScaler(),
    PolynomialFeatures(),
    Ridge())

    Как мы узнаем, какие степени полиномов нужно выбрать, выбирать ли полиномы или взаимодействия вообще? В идеале мы хотим выбрать значение параметра degree, основываясь на результатах классификации. С помощью нашего конвейера мы можем осуществить поиск значений параметра degree для полиномиальных преобразований значениями одновременно с поиском значений параметра alpha модели гребневой регрессии. Для этого мы задаем сетку параметров в необходимом формате: после каждого имени этапа следует двойной символ подчеркивания и соответствующий параметр:

[In 29]:
param_grid = {'polynomialfeatures__degree': [1, 2, 3],
              'ridge__alpha': [0.001, 0.01, 1, 10, 100]}

    Теперь мы можем запустить наш решетчатый поиск снова:

[In 30]:
grid = GridSearchCV(pipe, param_grid=param_grid, cv=5, n_jobs=-1)
grid.fit(X_train, y_train)

GridSearchCV(cv=5,
             estimator=Pipeline(steps=[('standardscaler', StandardScaler()),
                                       ('polynomialfeatures',
                                        PolynomialFeatures()),
                                       ('ridge', Ridge())]),
             n_jobs=-1,
             param_grid={'polynomialfeatures__degree': [1, 2, 3],
                         'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]})

    Результат перекрестной проверки можно визуализировать с помощью теплокарты (рисунок 1):

[In 31]:
plt.matshow(grid.cv_results_['mean_test_score'].reshape(3, -1),
            vmin=0, cmap="viridis")
plt.xlabel("ridge__alpha")
plt.ylabel("polynomialfeatures__degree")
plt.xticks(range(len(param_grid['ridge__alpha'])), param_grid['ridge__alpha'])
plt.yticks(range(len(param_grid['polynomialfeatures__degree'])),
           param_grid['polynomialfeatures__degree'])

plt.colorbar()

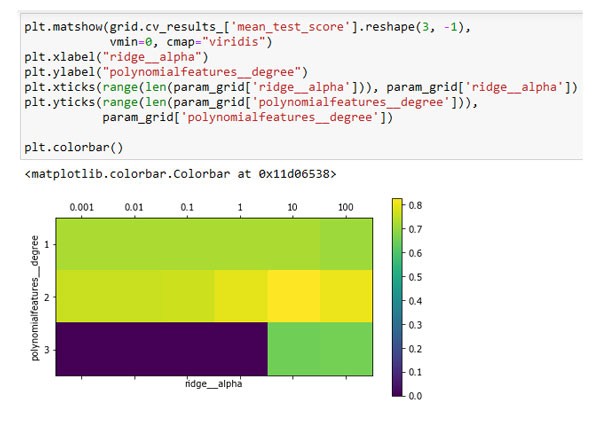
Рис.1. Теплокарта для усредненной правильности перекрестной проверки, выраженной в виде функции двух параметров: параметра degree для полиномиального преобразования и параметра alpha для гребневой регрессии

    Взглянув на результаты, полученные с помощью перекрестной проверки, мы можем увидеть, что степень полинома 2 помогает, однако степень полинома 3 дает гораздо худший результат, чем степень 1 или степень 2. Данный факт отражается в найденных наилучших параметрах:

[In 32]:
print("Наилучшие параметры: {}".format(grid.best_params_))

Наилучшие параметры: {'polynomialfeatures__degree': 2, 'ridge__alpha': 10}

[In 33]:
print("Правильность на тестовом наборе: {:.2f}".format(grid.score(X_test, y_test)))

Правильность на тестовом наборе: 0.77

    Давайте для сравнения запустим решетчатый поиск без полиномиального преобразования:

[In 34]:
param_grid = {'ridge__alpha': [0.001, 0.01, 1, 10, 100]}
pipe = make_pipeline(StandardScaler(), Ridge())
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)
print("Правильность без полином. преобразования: {:.2f}".format(
    grid.score(X_test, y_test)))

Правильность без полином. преобразования: 0.63

    Как мы и предполагали, анализируя результаты решетчатого поиска, приведенные на рисунке 1, отказ от использования полиномиальных признаков привел к существенно худшим результатам.

    Одновременный поиск параметров предварительной обработки и параметров модели является очень мощной стратегией. Однако имейте в виду, что GridSearchCV перебирает все возможные комбинации заданных параметров. Поэтому включение в сетку большего количества параметров ведет к экспоненциальному росту моделей.

    На следующем шаге мы рассмотрим выбор оптимальной модели с помошью решетчатого поиска.

Предыдущий шаг Содержание Следующий шаг