На этом шаге мы рассмотрим следующие примеры поиска решений:
- Минимизация расходов на перевозку
- Планирование штатного расписания
- Распределение ресурсов
- Оптимизация портфеля ценных бумаг
Минимизация расходов на перевозку
В этом примере производится поиск альтернативных способов перевозки грузов при сохранении минимальных общих расходов на перевозку (рис. 1).
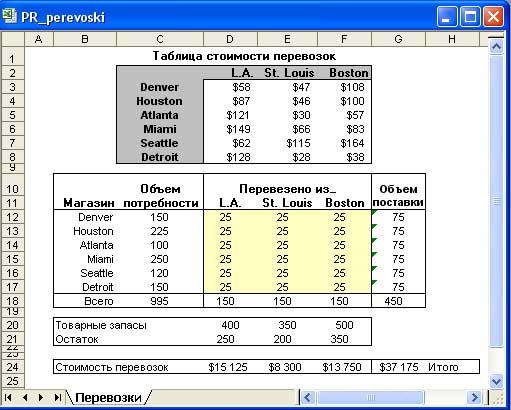
Рис.1. Пример минимизации расходов на перевозку товаров со складов в розничные магазины
Компания имеет склады в Лос-Анджелесе (L.A.), Сент-Луисе (St. Louis) и Бостоне (Boston). Заказы на перевозку грузов поступают из сети розничных магазинов, распределенных по всей территории США (Denver, Houston, Atlanta, Miami, Seattle, Detroit) и получающих товары с одного из складов.
Цель задачи — удовлетворить потребность в товарах, находящихся на складах, всех шести розничных магазинов и сохранить при этом общие расходы на перевозку на минимальном уровне.
Рабочий лист состоит из следующих частей:
- Таблица стоимости перевозок. Эта таблица, расположенная вверху листа, содержит информацию о стоимости перевозки единицы товара с каждого склада в каждый розничный магазин. Например, стоимость перевозки единицы товара из Лос-Анджелеса (L.A.) в Денвер (Denver) составляет $58.
- Потребность в товаре для каждого розничного магазина. Эта информация содержится в ячейках С12:С17. Например, для Денвера (Denver) нужно 150 единиц товара, для Хьюстона (Houston) — 225 и т.д. В ячейке С18 подсчитывается общая потребность в товарах.
- Количество перевезенного товара. В оттененном диапазоне D12:F17 находятся ячейки, значения в которых будут изменяться в результате выполнения процедуры поиска решения. Во всех ячейках установлено начальное значение 25. В столбце G содержатся формулы, суммирующие общее число единиц товара, который будет доставлен к каждому розничному магазину.
- Товарные запасы. В строке 20 содержится информация об общем количестве товаров, находящихся на каждом из складов. В строку 21 введены формулы, по которым вычитается количество перевезенных товаров (строка 18) из общего числа товаров, находящихся на складе. Например, в ячейке D21 располагается формула: = D20 - D18.
- Вычисляемая стоимость перевозок. Строка 24 содержит формулы, по которым вычисляется стоимость перевозок. В ячейке D24 содержится приведенная ниже формула, которая была скопирована в две ячейки справа: = СУММПРОИЗВ(D3:D8;D12:D17).
Эта формула позволяет вычислить общую стоимость перевозок с каждого склада. В ячейке G24 подводится общая стоимость перевозок для всех заказов.
Процедура поиска решения находит такие значения диапазона ячеек D12:F17, при которых розничный магазин будет получать желаемое количество товара и общая стоимость перевозок будет минимальна. Другими словами, нужно минимизировать значение, находящееся в ячейке G24, изменяя значения диапазона ячеек D12:D17 с учетом следующих ограничений:
- Количество необходимого товара для каждого розничного магазина должно равняться количеству перевезенного (другими словами, все заказы должны быть выполнены). Эти ограничения представляются следующими условиями:
C12 = G12 C14 = G14 C16 = G16 C13 = G13 C15 = G15 C17 = G17 - Значения в изменяемых ячейках не могут быть отрицательными. Иначе говоря, перевозка такого количества товара, значение которого отрицательно, бессмысленна. Эти ограничения представлены следующими условиями:
D12 >= 0 E12 >= 0 F12 >= 0 D13 >= 0 E13 >= 0 F13 >= 0 D14 >= 0 E14 >= 0 F14 >= 0 D15 >= 0 E15 >= 0 F15 >= 0 D16 >= 0 E16 >= 0 F16 >= 0 D17 >= 0 E17 >= 0 F17 >= 0 - Количество запасов в каждом магазине не должно быть отрицательным (нельзя перевезти то, чего нет в наличии). Это представлено следующими ограничивающими условиями:
D21 >= 0 E21 >= 0 F21 >= 0
После ввода всех ограничений в окне Поиск решения (рис. 2), следует нажать кнопку Выполнить.
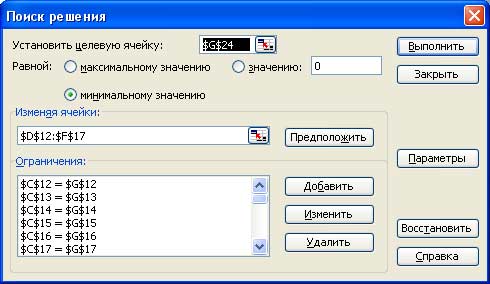
Рис.2. Диалоговое окно Поиск решения для рассматриваемой задачи
В результате (рис. 3) общая стоимость перевозок составит $55 515, при этом все потребности магазинов будут удовлетворены.
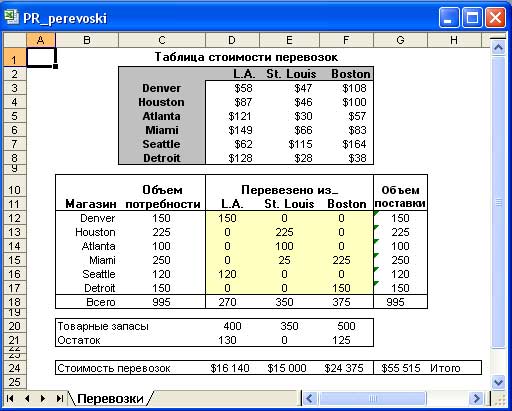
Рис.3. Результат выполнения процедуры поиска решения для рассматриваемой задачи
Файл с задачей о минимизации расходов на перевозку товаров можно взять здесь.
Вернуться к списку примеровПланирование штатного расписания
В этом примере рассматриваются вопросы планирования штатного расписания. Такие задачи обычно включают определение минимального количества людей, которое способно удовлетворить потребность в работниках в определенные дни или время дня. К ограничениям обычно относят общее количество дней или часов, которое должен отработать человек.
На рис. 4 показан рабочий лист, который позволяет провести элементарный анализ потребности в работниках.
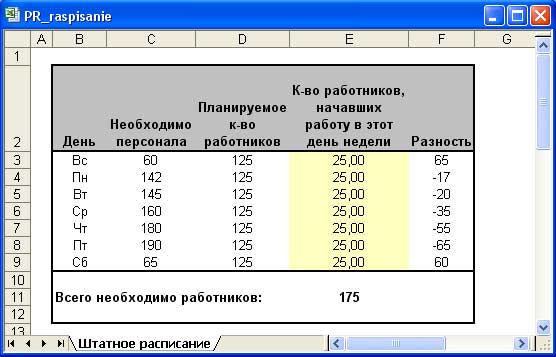
Рис.4. Модель планирования штатного расписания
Вопрос формулируется так: "Какое минимальное количество служащих требуется для удовлетворения ежедневной потребности в работниках?" В этой компании каждый служащий работает пять дней подряд. В результате служащие должны начинать свои пятидневные рабочие недели в разные дни недели.
Лист состоит из следующих частей:
- День. В столбце В находятся сокращенные названия дней недели.
- Потребность в персонале. В столбце С представлена численность персонала, которая необходима на каждый день недели. Как видно, потребность в персонале в зависимости от дня недели изменяется.
- Планируемое количество служащих. В столбце D находятся формулы, используюшие значения из столбца Е. В каждой формуле добавляется количество служащих, которые должны начать работу в текущий день, к количеству служащих,которые начинают работу в предыдущие четыре дня. Поскольку дни недели изменяются циклически, нельзя использовать одну и ту же формулу, просто копируя ее. Следовательно, формулы в разных ячейках столбца будут отличаться:
D3: =ЕЗ+Е9+Е8+Е7+Е6 D4: =Е4+Е3+Е9+Е8+Е7 D5: =Е5+Е4+Е3+Е9+Е8 D6: =Е6+Е5+Е4+Е3+Е9 D7: =Е7+Е6+Е5+Е4+Е3 D8: =Е8+Е7+Е6+Е5+Е4 D9: =Е9+Е8+Е7+Е6+Е5
- Изменяемые ячейки. Столбец Е содержит изменяемые ячейки — числа, которые
определяются с помощью процедуры поиска решений. Они заполнены начальными значениями, равными 25. Для изменяемых ячеек нужно выбирать
такие исходные значения, которые больше всего соответствуют ожидаемым.
- Разница. В столбце F содержатся формулы, по которым вычитается количество
необходимого персонала из планируемого количества людей. Это позволяет определить избыток или недостаток персонала. В ячейку F3 введена формула = D3 - C3, которая копируется в шесть остальных ячеек столбца.
- Общая потребность в персонале. По формуле в ячейке Е11 суммируется количество служащих, которые должны работать на протяжении всей рабочей недели. Формула для вычисления следующая: = СУММ(E3:E9). Это значение и будет минимизироваться.
Ограничения задачи: численность служащих, планируемая на каждый день, должна быть больше или равна необходимому количеству. Если значения, находящиеся во всех ячейках столбца F, больше или равны нулю, то ограничение выполняется.
| F3 >= 0 | F4 >= 0 | F5 >= 0 | F6 >= 0 |
|---|---|---|---|
| F7 >= 0 | F8 >= 0 | F9 >= 0 |
После ввода данных и формул выберите команду Сервис | Поиск решения и укажите, что необходимо минимизировать значение, находящееся в ячейке E11, с помощью изменяемых ячеек ЕЗ:Е9. Затем введите ограничения и нажмите кнопку Выполнить.
Найденное решение, показанное на рис. 5, означает, что количество служащих, равное 188, удовлетворяет общей потребности в работниках и при этом не будет никаких отклонений от требуемого количества на каждый день.
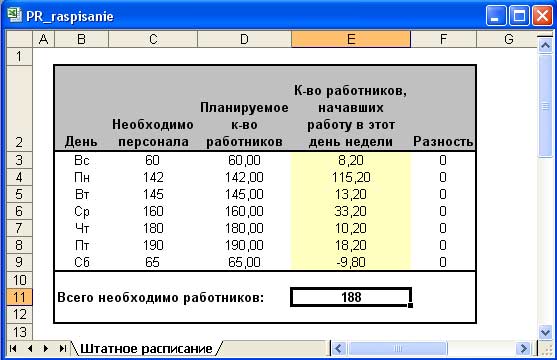
Рис.5. Результат выполнения процедуры поиска решения для задачи планирования штатного расписания
Если рассмотреть результаты, то можно обратить внимание на несколько неточностей:
- В полученном решении используются нецелые значения, определяющие количество служащих.
- В полученном решении используются отрицательные значения, определяющие количество служащих.
Исправить данные ошибки можно путем введения ограничений:
- Для каждой ячейки диапазона E3:E9 нужно указать ограничение цел (рис. 6).
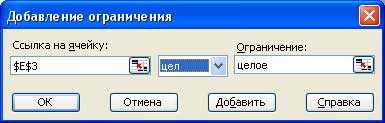
Рис.6. Диалоговое окно Добавление ограничения для определения целочисленного ограничения - Для каждой ячейки диапазона E3:E9 нужно указать ограничение >= 0.
После добавления ограничений получим следующий результат (рис. 7):
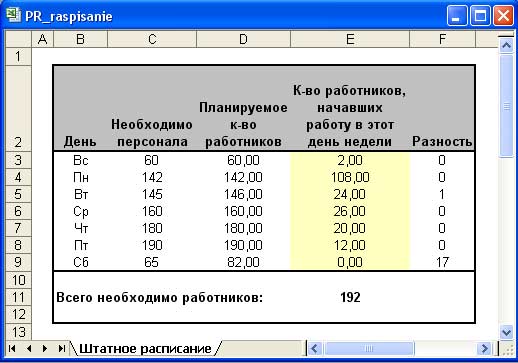
Рис.7. Результат выполнения процедуры поиска решения после ввода дополнительных ограничений
Файл с задачей планирования штатного расписания можно взять здесь.
Вернуться к списку примеровРаспределение ресурсов
В данном примере предлагается найти оптимальный объем производства продукции в зависимости от имеющегося количества ресурсов. На рис. 8 показан пример расчета для компании по производству игрушек.
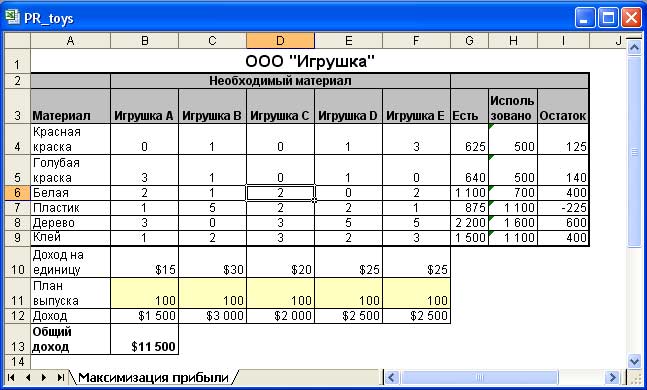
Рис.8. Максимизация прибыли в условиях ограниченности ресурсов
Компания производит 5 видов игрушек, для которых используются 6 видов материала в различном количестве. В столбце G показаны текущие запасы материалов. В строке 10 показан доход от производства одной игрушки каждого вида. Количество произведенных игрушек находится в диапазоне B11:F11 (значения в ячейках диапазона будут определяться с помощью процедуры поиска решения).
Цель задачи - так распределить ресурсы, чтобы максимизировать значение общей прибыли, которое находится в ячейке B13.
Ограничения задачи:
- На выпуск продукции должно уходить только имеющееся в наличии количество ресурсов. Т.е. нужно указать, что значения в каждой ячейке столбца I больше или равны нулю.
- Количество произведенного не должно быть отрицательным. Т.е. значения в каждой ячейке строки 11 больше или равны нулю.
На рис. 9 показаны результаты, полученные с помощью процедуры поиска решения. В таблице отображается количество продукции каждого вида, которое нужно выпустить, чтобы получить максимальную прибыль ($12 365).
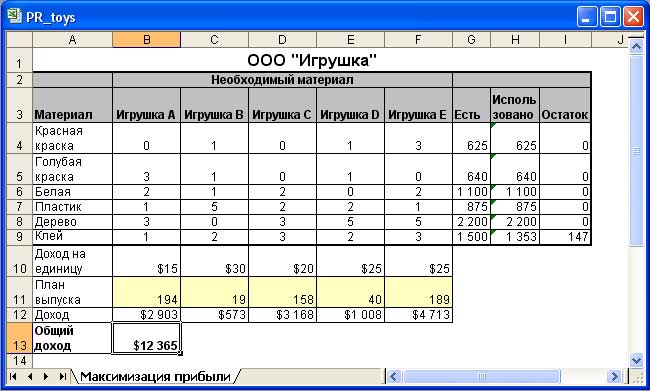
Рис.9. Результат выполнения процедуры поиска решения для максимизации прибыли в условиях ограниченности ресурсов
Файл с задачей о распределении ресурсов можно взять здесь.
Вернуться к списку примеровОптимизация портфеля ценных бумаг
В примере рассматривается применение процедуры поиска решения для максимизации дохода от портфеля ценных бумаг. Портфель содержит несколько инвестиционных проектов, каждый из которых приносит различный доход. Существует возможность использовать дополнительные ограничения для снижения риска потерь и правильного распределения капитала.
В примере используется гипотетическая модель кредитного союза - финансовая компания, которая принимает деньги от своих членов и выдает ссуды под проценты другим членам, выдает кредиты банкам и осуществляет некоторые виды инвестирования. Часть дохода перераспределяется между членами компании в виде дивидендов, которые зависят от доли их депозитных вкладов. Этот гипотетический кредитный союз должен придерживаться правил, касающихся инвестиций. Кроме того, правление может установить свои правила, которые составляют ограничения для данной задачи. На рис. 10 показана рабочая книга, созданная для решения задачи максимизации доходов от инвестиций кредитного союза.
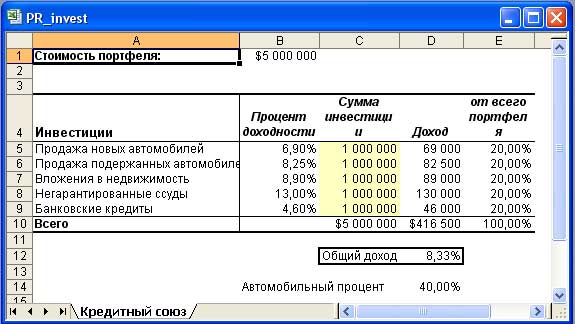
Рис.10. Задача максимизации доходов от инвестиций кредитного союза
Ограничения задачи:
- Сумма инвестиций в предприятия, торгующие новыми автомобилями, должна быть, по крайней мере, в 3 раза больше суммы инвестиций в предприятия, торгующие подержанными автомобилями, поскольку торговля подержанными автомобилями более рискованное дело. Ограничение записывается так: C5 >= C6 * 3
- Ссуды на автомобили должны составлять, по крайней мере, 15% от полной суммы портфеля. Ограничение записывается так: D14 >= 0,15
- Негарантированые ссуды должны составлять не более 25% от суммы портфеля. Ограничение записывается так: E8 <= 0,25
- Банковские кредиты должны составлять, по крайней мере, 10% от суммы портфеля. Ограничение записывается так: E9 >= 0,1
- Все инвестиции должны быть больше или равны нулю.
Изменяемые ячейки - C5:C9, а цель задачи - максимизировать общий доход, указанный в ячейке D12. В изменяемые ячейки введено начальное значение 1 000 000. Если запустить процедуру поиска решения с данными параметрами, то будет получен результат, показанный на рис. 11.
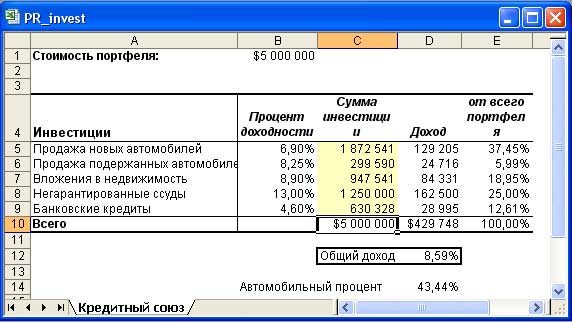
Рис.11. Результат оптимизации портфеля ценных бумаг
Файл с задачей об оптимизации портфеля ценных бумаг можно взять здесь.
Вернуться к списку примеровНа следующем шаге мы рассмотрим пакет анализа.
