На этом шаге мы приведем основные топологии сетей передачи данных.
В мультикомпьютерах для организации взаимодействия, синхронизации и взаимоисключения параллельно выполняемых процессов используется передача данных между процессорами вычислительной среды. Временные задержки при передаче данных по линиям связи могут оказаться существенными (по сравнению с быстродействием процессоров), и, как результат, коммуникационная трудоемкость алгоритма оказывает заметное влияние на выбор параллельных способов решения задач.
Примеры топологий сети передачи данных
Структура линий коммутации между процессорами вычислительной системы (топология сети передачи данных) определяется, как правило, с учетом возможностей эффективной технической реализации. Немаловажную роль при выборе структуры сети играет и анализ интенсивности информационных потоков при параллельном решении наиболее распространенных вычислительных задач. К числу типовых топологий обычно относят следующие схемы коммуникации процессоров (рисунок 1):
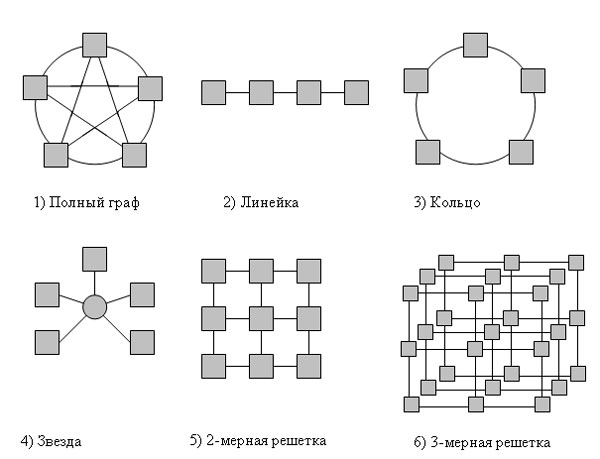
Рис.1. Примеры топологий многопроцессорных вычислительных систем
- полный граф - система, в которой между любой парой процессоров существует прямая линия связи. Такая топология обеспечивает минимальные затраты при передаче данных, однако является сложно реализуемой при большом количестве процессоров;
- линейка - система, в которой все процессоры перенумерованы по порядку и каждый процессор, кроме первого и последнего, имеет линии связи только с двумя соседними (с предыдущим и последующим) процессорами. Такая схема является, с одной стороны, просто реализуемой, c другой стороны, соответствует структуре передачи данных при решении многих вычислительных задач (например, при организации конвейерных вычислений);
- кольцо - данная топология получается из линейки процессоров соединением первого и последнего процессоров линейки;
- звезда - система, в которой все процессоры имеют линии связи с некоторым управляющим процессором. Данная топология является эффективной, например, при организации централизованных схем параллельных вычислений;
- решетка - система, в которой граф линий связи образует прямоугольную сетку (обычно двух- или трехмерную). Подобная топология может быть достаточно просто реализована и, кроме того, эффективно использована при параллельном выполнении многих численных алгоритмов (например, при реализации методов анализа математических моделей, описываемых дифференциальными уравнениями в частных производных);
- гиперкуб - данная топология представляет собой частный случай структуры решетки, когда по каждой размерности сетки
имеется только два процессора (т.е. гиперкуб содержит 2N процессоров при размерности N). Такой вариант организации сети
передачи данных достаточно широко распространен на практике и характеризуется следующим рядом отличительных признаков:
- Два процессора имеют соединение, если двоичные представления их номеров имеют только одну различающуюся позицию;
- В N-мерном гиперкубе каждый процессор связан ровно с N соседями;
- N-мерный гиперкуб может быть разделен на два (N-1)-мерных гиперкуба (всего возможно N различных таких разбиений);
- Кратчайший путь между двумя любыми процессорами имеет длину, совпадающую с количеством различающихся битовых значений в номерах процессоров (данная величина известна как расстояние Хэмминга).
Схема линий передачи данных может реализовываться на аппаратном уровне, а может быть обеспечена на основе имеющейся физической топологии при помощи соответствующего программного обеспечения. Введение виртуальных (программно-реализуемых) топологий способствует мобильности разрабатываемых параллельных программ и снижает затраты на программирование.
На следующем шаге мы рассмотрим топологию сети вычислительных кластеров и ее характеристики.
