На этом шаге мы рассмотрим некоторые представления топологии коммуникационной среды.
Ряд алгоритмов передачи данных допускает более простое изложение при использовании вполне определенных топологий сети межпроцессорных соединений. Кроме того, многие методы коммуникации могут быть получены при помощи того или иного логического представления исследуемой топологии. Как результат, важным моментом при организации параллельных вычислений является возможность логического представления разнообразных топологий на основе конкретных (физических) межпроцессорных структур.
Способы логического представления (отображения) топологий характеризуются следующими тремя основными характеристиками:
- уплотнение дуг, выражаемое как максимальное количество дуг логической топологии, которые отображаются в одну линию передачи физической топологии;
- удлинение дуг, определяемое как путь максимальной длины физической топологии, на который отображается дуга логической топологии;
- увеличение вершин, вычисляемое как отношение количества вершин в логической и физической топологиях.
Представление кольцевой топологии в виде гиперкуба
Установление соответствия между кольцевой топологией и гиперкубом может быть выполнено с помощью двоичного рефлексивного кода Грея G(i, N), определяемого в соответствии с выражениями:
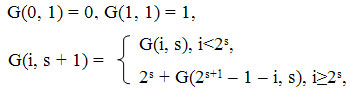
где i задает номер значения в коде Грея, а N есть длина этого кода. Для иллюстрации подхода в таблице показывается отображение кольцевой топологии на гиперкуб для сети из p=8 процессоров.
Важное свойство кода Грея: соседние значения G(i, N) и G(i+1, N) имеют только одну различающуюся битовую позицию. Как результат, соседние вершины в кольцевой топологии отображаются на соседние процессоры в гиперкубе.
| Код Грея для N=1 | Код Грея для N=2 | Код Грея для N=3 | Номера процессоров | |
|---|---|---|---|---|
| гиперкуба | кольца | |||
| 0 | 0 0 | 0 0 0 | 0 | 0 |
| 1 | 0 1 | 0 0 1 | 1 | 1 |
| 1 1 | 0 1 1 | 3 | 2 | |
| 1 0 | 0 1 0 | 2 | 3 | |
| 1 1 0 | 6 | 4 | ||
| 1 1 1 | 7 | 5 | ||
| 1 0 1 | 5 | 6 | ||
| 1 0 0 | 4 | 7 | ||
Отображение топологии решетки на гиперкуб
Отображение топологии решетки на гиперкуб может быть выполнено в рамках подхода, использованного для кольцевой структуры сети.
Тогда для отображения решетки 2r x 2s на гиперкуб размерности N=r+s можно принять правило, что элементу решетки с координатами (i, j) соответствует процессор гиперкуба с номером G(i,r)||G(j,s), где операция || означает конкатенацию кодов Грея.
На следующем шаге мы рассмотрим оценку трудоемкости операций передачи данных.
