На этом шаге мы рассмотрим начальные этапы разработки параллельных алгоритмов.
Рассмотрим более подробно методику разработки параллельных алгоритмов. Для демонстрации приводимых рекомендаций далее будет использоваться учебная задача поиска максимального значения среди элементов матрицы A (такая задача возникает, например, при численном решении систем линейных уравнений для определения ведущего элемента метода Гаусса):
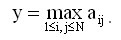
Разделение вычислений на независимые части
Это первый шаг в решении поставленной задачи.
Выбор способа разделения вычислений на независимые части основывается на анализе вычислительной схемы решения исходной задачи. Требования, которым должен удовлетворять выбираемый подход, обычно состоят в обеспечении равного объема вычислений в выделяемых подзадачах и минимума информационных зависимостей между этими подзадачами (при прочих равных условиях нужно отдавать предпочтение редким операциям передачи сообщений большего размера по сравнению с частыми пересылками данных небольшого объема). В общем случае, проведение анализа и выделение задач представляет собой достаточно сложную проблему - ситуацию помогает разрешить существование двух часто встречающихся типов вычислительных схем.
Для большого класса задач вычисления сводятся к выполнению однотипной обработки большого набора данных - к такому классу задач относятся, например, матричные вычисления, численные методы решения уравнений в частных производных и др. В этом случае говорят, что существует параллелизм по данным, и выделение подзадач сводится к разделению имеющихся данных. Так, например, для рассматриваемой учебной задачи поиска максимального значения при формировании подзадач исходная матрица может быть разделена на отдельные строки (или последовательные группы строк) - так называемая ленточная схема разделения данных - либо на прямоугольные наборы элементов - блочная схема разделения данных (рисунок 1).
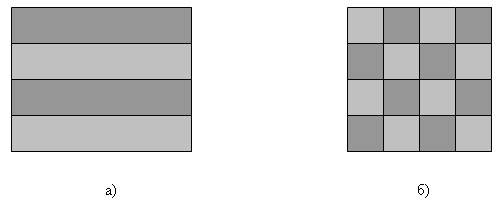
Рис.1. Разделение данных матрицы: а) ленточная схема, б) блочная схема
Для большого количества решаемых задач разделение вычислений по данным приводит к порождению одно-, дву- и трехмерных наборов подзадач, в которых информационные связи существуют только между ближайшими соседями (такие схемы обычно именуются сетками или решетками).
Для другой части задач вычисления могут состоять в выполнении разных операций над одним и тем же набором данных - в этом случае говорят о существовании функционального параллелизма (в качестве примеров можно привести задачи обработки последовательности запросов к информационным базам данных, вычисления с одновременным применением разных алгоритмов расчета и т.п.). Очень часто функциональная декомпозиция может быть использована для организации конвейерной обработки данных (так, например, при выполнении каких-либо преобразований данных вычисления могут быть сведены к функциональной последовательности ввода, обработки и сохранения данных).
Важный вопрос при выделении подзадач состоит в выборе нужного уровня декомпозиции вычислений. Формирование максимально возможного количества подзадач обеспечивает использование предельно достижимого уровня параллелизма решаемой задачи, однако затрудняет анализ параллельных вычислений. Применение при декомпозиции вычислений только достаточно "крупных" подзадач приводит к ясной схеме параллельных вычислений, однако может затруднить эффективное использование достаточно большого количества процессоров. Возможное разумное сочетание этих двух подходов может состоять в применении в качестве конструктивных элементов декомпозиции только тех подзадач, для которых методы параллельных вычислений являются известными. Так, например, при анализе задачи матричного умножения в качестве подзадач можно использовать методы скалярного произведения векторов или алгоритмы матрично-векторного произведения. Подобный промежуточный способ декомпозиции вычислений позволит обеспечить и простоту представления вычислительных схем, и эффективность параллельных расчетов. Выбираемые подзадачи при таком подходе будем именовать далее базовыми, которые могут быть элементарными (неделимыми), если не допускают дальнейшего разделения, или составными - в противном случае.
Для рассматриваемой задачи достаточный уровень декомпозиции может состоять, например, в разделении матрицы на множество отдельных строк и получении на этой основе набора подзадач поиска максимальных значений в отдельных строках; порождаемая при этом структура информационных связей соответствует линейному графу.
Для оценки корректности этапа разделения вычислений на независимые части можно воспользоваться контрольным списком вопросов:
- Выполненная декомпозиция не увеличивает объем вычислений и необходимый объем памяти?
- Возможна ли при выбранном способе декомпозиции равномерная загрузка всех имеющихся процессоров?
- Достаточно ли выделенных частей процесса вычислений для эффективной загрузки имеющихся процессоров (с учетом возможности увеличения их количества)?
Перейдем ко второму шагу в решении задачи.
Выделение информационных зависимостей
При наличии вычислительной схемы решения задачи после выделения базовых подзадач определение информационных зависимостей между ними обычно не вызывает больших затруднений. При этом, однако, следует отметить, что на самом деле этапы выделения подзадач и информационных зависимостей достаточно сложно поддаются разделению. Выделение подзадач должно происходить с учетом возникающих информационных связей, после анализа объема и частоты необходимых информационных обменов между подзадачами может потребоваться повторение этапа разделения вычислений.
При проведении анализа информационных зависимостей между подзадачами следует различать:
- локальные и глобальные схемы передачи данных - для локальных схем передачи данных в каждый момент времени выполняются только между небольшим числом подзадач (располагаемых, как правило, на соседних процессорах), для глобальных операций передачи данных в процессе коммуникации принимают участие все подзадачи;
- структурные и произвольные способы взаимодействия - для структурных способов организация взаимодействий приводит к формированию некоторых стандартных схем коммуникации (например, в виде кольца, прямоугольной решетки и т. д.), для произвольных структур взаимодействия схема выполняемых операций передач данных не носит характера однородности;
- статические или динамические схемы передачи данных - для статических схем моменты и участники информационного взаимодействия фиксируются на этапах проектирования и разработки параллельных программ, для динамического варианта взаимодействия структура операции передачи данных определяется в ходе выполняемых вычислений;
- синхронные и асинхронные способы взаимодействия - для синхронных способов операции передачи данных выполняются только при готовности всех участников взаимодействия и завершаются только после полного окончания всех коммуникационных действий, при асинхронном выполнении операций участники взаимодействия могут не дожидаться полного завершения действий по передаче данных. Для представленных способов взаимодействия достаточно сложно выделить предпочтительные формы организации передачи данных: синхронный вариант, как правило, более прост для применения, в то время как асинхронный способ часто позволяет существенно снизить временные задержки, вызванные операциями информационного взаимодействия.
Для оценки правильности этапа выделения информационных зависимостей можно воспользоваться контрольным списком вопросов:
- Соответствует ли вычислительная сложность подзадач интенсивности их информационных взаимодействий?
- Является ли одинаковой интенсивность информационных взаимодействий для разных подзадач?
- Является ли схема информационного взаимодействия локальной?
- Не препятствует ли выявленная информационная зависимость параллельному решению подзадач?
На следующем шаге мы закончим изучение этого вопроса.
