На этом шаге мы приведем анализ эффективности алгоритма Гаусса.

Пусть, как и ранее, n есть порядок решаемой системы линейных уравнений, а р, р<n, обозначает число используемых процессоров. Тем самым, матрица коэффициентов А имеет размер n*n и, соответственно, n/p есть размер полосы матрицы А на каждом процессоре.

Прежде всего, несложно показать, что общее время выполнения последовательного варианта метода Гаусса составляет:

T₁ = 2n³/3 + n².

Определим теперь сложность параллельного варианта метода Гаусса. При выполнении прямого хода алгоритма на каждой итерации для выбора ведущей строки каждый процессор должен осуществить выбор максимального значения в столбце с исключаемой неизвестной в пределах своей полосы. Начальный размер полос на процессорах равен n/p, но по мере исключения неизвестных количество строк в полосах для обработки постепенно сокращается. Текущий размер полос приближенно можно оценить как (n-i)/p, где i, 0<=i<n-1, есть номер выполняемой итерации прямого хода метода Гаусса. Далее после сбора полученных максимальных значений, определения и рассылки ведущей строки, каждый процессор должен выполнить вычитание ведущей строки из каждой строки оставшейся части строк своей полосы матрицы A. Количество элементов строки, подлежащих обработке, также сокращается при исключении неизвестных, и текущее число элементов строки для вычислений оценивается величиной (n-i). Тем самым, сложность процедуры вычитания строк оценивается как 2*(n-i) операций (перед вычитанием ведущая строка умножается на масштабирующую величину a_ik/a_ii). С учетом выполняемого количества итераций, общее число операций параллельного варианта прямого хода метода Гаусса определяется выражением:

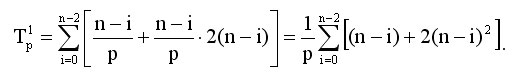
На каждой итерации обратного хода алгоритма Гаусса после рассылки вычисленного значения очередной неизвестной каждый процессор должен обновить значения правых частей для всех строк, расположенных на этом процессоре. Отсюда следует, что трудоемкость параллельного варианта обратного хода алгоритма Гаусса оценивается как величина:

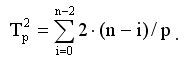
Просуммировав полученные выражения, можно получить:

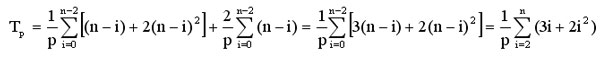
Как результат выполненного анализа, показатели ускорения и эффективности параллельного варианта метода Гаусса могут быть определены при помощи соотношений следующего вида:

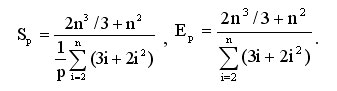
Полученные соотношения имеют достаточно сложный вид для оценивания. Вместе с тем можно показать, что сложность параллельного алгоритма имеет порядок ~(2n³/3)/p, и, тем самым, балансировка вычислительной нагрузки между процессорами в целом является достаточно равномерной.

Дополним сформированные показатели вычислительной сложности метода Гаусса оценкой затрат на выполнение операций передачи данных между процессорами. При выполнении прямого хода на каждой итерации для определения ведущей строки процессоры обмениваются локально найденными максимальными значениями в столбце с исключаемой переменной. Всего для выполнения такой операции требуется log₂p шагов, что с учетом количества итераций позволяет оценить время, необходимое для проведения операций редукции, при помощи следующего выражения:

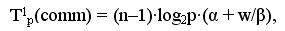
где, как и ранее, альфа - латентность сети передачи данных, бета - пропускная способность сети, w - размер пересылаемого элемента данных.

Далее также на каждой итерации прямого хода метода Гаусса выполняется рассылка выбранной ведущей строки. Сложность данной операции передачи данных является равной:

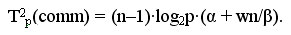
При выполнении обратного хода алгоритма Гаусса на каждой итерации осуществляется рассылка между всеми процессорами вычисленного значения очередной неизвестной. Общее время, необходимое для выполнения подобных действий, можно оценить как:

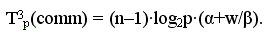
Подводя итог, с учетом всех полученных выражений, трудоемкость параллельного варианта метода Гаусса составляет:

где

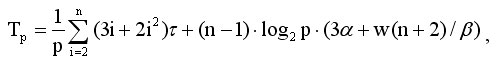
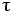есть время выполнения базовой вычислительной операции.

На следующем шаге мы рассмотрим результаты вычислительных экспериментов.

Предыдущий шаг Содержание Следующий шаг