Шаг 58.
Параллельные алгоритмы. Пример 4. Параллельные алгоритмы обработки графов. Параллельные алгоритмы. Алгоритм Прима

    На этом шаге мы рассмотрим особенности использования алгоритма Прима.

Разделение вычислений на независимые части

    Оценим возможности параллельного выполнения рассмотренного алгоритма нахождения минимального охватывающего дерева. Итерации метода должны выполняться последовательно и, тем самым, не могут быть распараллелены. С другой стороны, выполняемые на каждой итерации алгоритма действия являются независимыми и могут реализовываться одновременно. Так, например, определение величин d_i может осуществляться для каждой вершины графа в отдельности, нахождение дуги минимального веса может быть реализовано по каскадной схеме и т.д.

    Распределение данных между процессорами вычислительной системы должно обеспечивать независимость перечисленных операций алгоритма Прима. В частности, это может быть реализовано, если каждая вершина графа располагается на процессоре вместе со всей связанной с вершиной информацией. Соблюдение данного принципа приводит к тому, что при равномерной загрузке каждый процессор P_j, 1<=j<=p, должен содержать:

    1. Набор вершин

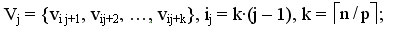
    2. Соответствующий этому набору блок из k величин

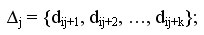
    3. Вертикальную полосу матрицы смежности графа G из k соседних столбцов

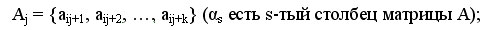
    4. Общую часть набора V_j и формируемого в процессоре вычислений множества вершин V_T.

    Можно заключить, что базовой подзадачей в параллельном алгоритме Прима может служить процедура вычисления блока значений 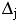для вершин V_j матрицы смежности А графа G.

Выделение информационных зависимостей

    С учетом выбора базовых подзадач общая схема параллельного выполнения алгоритма Прима будет состоять в следующем:

1. Определяется вершина t графа G, имеющая дугу минимального веса до множества V_T; для выбора такой вершины необходимо осуществить поиск минимума в наборах величин d_i, имеющихся на каждом из процессоров, и выполнить сборку полученных значений на одном из процессоров;
2. Номер выбранной вершины для включения в охватывающее дерево передается всем процессорам;
3. Обновляются наборы величин d_i с учетом добавления новой вершины.

    Таким образом, в ходе параллельных вычислений между процессорами выполняются два типа информационных взаимодействий - сбор данных от всех процессоров на одном из процессоров и передача сообщений от одного процессора всем процессорам вычислительной системы.

Масштабирование и распределение подзадач по процессорам

    В соответствии с определением количество базовых подзадач всегда соответствует числу имеющихся процессоров и, тем самым, проблема масштабирования для параллельного алгоритма не возникает.

    Распределение подзадач между процессорами должно учитывать характер выполняемых в алгоритме Прима коммуникационных операций. Для эффективной реализации требуемых информационных взаимодействий между базовыми подзадачами топология сети передачи данных должна иметь структуру гиперкуба или полного графа.

    На следующем шаге мы проанализируем эффективность использования алгоритма Флойда.

Предыдущий шаг Содержание Следующий шаг