На этом шаге мы рассмотрим функцию, реализующую такой поиск.

    Существует более быстрый способ поиска, чем просмотр всех элементов. Но при этом требуется заранее знать кое-что о последовательности структуры данных. Если известно, что структура отсортирована и мы можем мгновенно получить доступ к любому ее элементу по его индексу, то можно выполнить бинарный поиск. Если исходить из этого критерия, то отсортированный список Python - идеальный кандидат для бинарного поиска.

    При бинарном поиске средний элемент в отсортированном диапазоне элементов проверяется и сравнивается с искомым элементом. По результатам сравнения диапазон поиска уменьшается наполовину, после чего процесс повторяется. Рассмотрим его на конкретном примере.

    Предположим, что у нас есть список отсортированных по алфавиту слов ("заяц", "зебра", "кенгуру", "кошка", "крыса", "лама", "собака") и мы ищем слово "крыса".

1. Мы определили, что средним элементом в списке из семи слов является "кошка".

2. Теперь можем определить, что по алфавиту "крыса" идет после "кошки", поэтому она должна находиться (это неточно) в той половине списка, которая следует после "кошки". (Если бы мы нашли "крысу" на этом шаге, то могли бы вернуть местонахождение этого слова; если бы обнаружили, что искомое слово стояло перед средним словом, которое мы проверяли, то могли бы быть уверены, что оно находится в половине списка до "кошки".)

3. Мы могли бы повторить пункты 1 и 2 для той половины списка, в которой, как уже знаем, вероятно, находится слово "крыса". По сути, эта половина становится новым исходным списком. Указанные пункты выполняются повторно до тех пор, пока "крыса" не будет найдена или же диапазон, в котором выполняется поиск, больше не будет содержать элементов для поиска, то есть слова "крыса" не будет существовать в заданном списке слов.

    Процедура бинарного поиска проиллюстрирована на рисунке 1.Обратите внимание на то, что, в отличие от линейного поиска, здесь не подразумевается проверка каждого элемента.

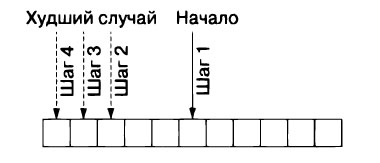
Рис.1. В худшем случае при бинарном поиске придется просматривать только lg(n) элементов списка

    При бинарном поиске пространство поиска постоянно сокращается вдвое, поэтому в худшем случае время выполнения поиска составляет O(lg n). Однако здесь есть своеобразная ловушка. В отличие от линейного поиска для бинарного требуется отсортированная структура данных, а сортировка требует времени. На самом деле сортировка занимает время O(n lg n) даже при использовании лучших алгоритмов. Если мы собираемся запустить поиск только один раз, а исходная структура данных не отсортирована, возможно, имеет смысл просто выполнить линейный поиск. Но если поиск должен выполняться много раз, то стоит потратить время на сортировку, чтобы каждый отдельный поиск занял значительно меньше времени.

    Написание функции бинарного поиска для гена и кодона мало отличается от написания функции для любого другого типа данных, поскольку объекты типа Codon можно сравнивать между собой, а тип Gene - это просто список.

def binary_contains(gene: Gene, key_codon: Codon) -> bool:
    low: int = 0
    high: int = len(gene) - 1
    while low <= high:  # пока еще есть место для поиска
        mid: int = (low + high) // 2
        if gene[mid] < key_codon:
            low = mid + 1
        elif gene[mid] > key_codon:
            high = mid - 1
        else:
            return True
    return False

    Рассмотрим выполнение этой функции построчно:

    low: int = 0
    high: int = len(gene) - 1

    Начнем поиск с диапазона, который охватывает весь список (ген):

    while low <= high:  # пока еще есть место для поиска

    Мы продолжаем поиск до тех пор, пока существует диапазон для поиска. Когда low станет больше, чем high, это будет означать, что в списке не осталось фрагментов для просмотра:

        mid: int = (low + high) // 2

    Вычисляем среднее значение mid, используя целочисленное деление и простую формулу вычисления среднего, знакомую еще по начальной школе:

        if gene[mid] < key_codon:
            low = mid + 1

    Если искомый элемент находится после среднего элемента текущего диапазона, то изменяем диапазон, который будем рассматривать на следующей итерации цикла, перемещая low на следующий после текущего среднего элемента. Именно на этом шаге мы вдвое сокращаем диапазон поиска для следующей итерации:

        elif gene[mid] > key_codon:
            high = mid - 1

    Если искомый элемент меньше, чем средний, мы точно так же делим диапазон пополам и выбираем другое направление:

        else:
            return True

    Если рассматриваемый элемент не меньше и не больше, чем средний, это означает, что мы его нашли! И конечно же, если в цикле закончились итерации, то возвращаем False (здесь это повторять не будем), указывая, что элемент не был найден.

    Мы можем попробовать запустить функцию с тем же геном и кодоном, но необходимо помнить, что сначала нужно отсортировать данные.

my_sorted_gene: Gene = sorted(my_gene)
print(binary_contains(my_sorted_gene, acg))  # True
print(binary_contains(my_sorted_gene, gat))  # FaLse

Для построения эффективной процедуры бинарного поиска можно воспользоваться модулем bisect из стандартной библиотеки Python: https://docs.python.org/3/library/bisect.html.

    На следующем шаге мы рассмотрим параметризованный пример.

Предыдущий шаг Содержание Следующий шаг