На этом шаге мы приведем реализацию алгоритма поиска в глубину.
Понадобится учесть еще один момент, прежде чем можно будет приступить к реализации DFS. Требуется класс Node, с помощью которого мы станем отслеживать переход из одного состояния в другое (или из одного места лабиринта в другое) во время поиска. Node можно представить как обертку вокруг состояния. В случае прохождения лабиринта эти состояния имеют тип MazeLocation. Будем считать Node состоянием, унаследованным от parent. Кроме того, для класса Node мы определим свойства cost и heuristic и реализуем метод __lt__(), чтобы использовать его позже в алгоритме А* (файл generic_search.py):
class Node(Generic[T]): def __init__(self, state: T, parent: Optional[Node], cost: float = 0.0, heuristic: float = 0.0) -> None: self.state: T = state self.parent: Optional[Node] = parent self.cost: float = cost self.heuristic: float = heuristic def __lt__(self, other: Node) -> bool: return (self.cost + self.heuristic) < (other.cost + other.heuristic)
Тип Optional указывает, что переменная может ссылаться на значение параметризованного типа или на None.
Строка
from __future__ import annotations
В процессе поиска в глубину нужно отслеживать две структуры данных:
- стек рассматриваемых состояний (мест), который мы назовем frontier, и
- набор уже просмотренных состояний - explored.
def dfs(initial: T, goal_test: Callable[[T], bool], successors: Callable[[T], List[T]]) -> Optional[Node[T]]: # frontier - то, что нам нужно проверить frontier: Stack[Node[T]] = Stack() frontier.push(Node(initial, None)) # explored - то, где мы уже были explored: Set[T] = {initial} # продолжаем, пока есть что просматривать while not frontier.empty: current_node: Node[T] = frontier.pop() current_state: T = current_node.state # если мы нашли искомое, заканчиваем if goal_test(current_state): return current_node # проверяем, куда можно двинуться дальше и что мы еще не исследовали for child in successors(current_state): if child in explored: # пропустить состояния, которые уже исследовали continue explored.add(child) frontier.push(Node(child, current_node)) return None # все проверили, пути к целевой точке не нашли
Если dfs() завершается успешно, то возвращается Node, в котором инкапсулировано искомое состояние. Для того чтобы восстановить путь от начала до целевой ячейки, нужно двигаться в обратном направлении от этого Node к его предкам, используя свойство parent (файл generic_search.py):
def node_to_path(node: Node[T]) -> List[T]: path: List[T] = [node.state] # двигаемся назад, от конца к началу while node.parent is not None: node = node.parent path.append(node.state) path.reverse() return path
В целях отображения полезно будет разметить лабиринт с указанием успешного пути, начального и конечного положений. Также хорошо иметь возможность удалить путь, чтобы можно было применить разные алгоритмы поиска для одного и того же лабиринта. Для этого в исходном файле, где описан класс Maze, добавим следующие два метода:
def mark(self, path: List[MazeLocation]):
for maze_location in path:
self._grid[maze_location.row][maze_location.column] = Cell.PATH
self._grid[self.start.row][self.start.column] = Cell.START
self._grid[self.goal.row][self.goal.column] = Cell.GOAL
def clear(self, path: List[MazeLocation]):
for maze_location in path:
self._grid[maze_location.row][maze_location.column] = Cell.EMPTY
self._grid[self.start.row][self.start.column] = Cell.START
self._grid[self.goal.row][self.goal.column] = Cell.GOAL
Это было долгое путешествие, но оно подходит к копну - мы готовы пройти по лабиринту.
if __name__ == "__main__": # Тестирование DFS m: Maze = Maze() print(m) solution1: Optional[Node[MazeLocation]] = dfs(m.start, m.goal_test, m.successors) if solution1 is None: print("Поиском в глубину решение не найдено!") else: path1: List[MazeLocation] = node_to_path(solution1) m.mark(path1) print(m) m.clear(path1)
Успешное решение будет выглядеть примерно так:
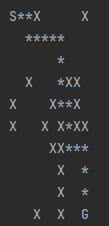
Рис.1. Результат работы приложения
Звездочки обозначают путь от начальной до конечной точки, который нашла функция поиска в глубину. Помните: поскольку все лабиринты генерируются случайным образом, не для каждого из них существует решение.
На следующем шаге мы рассмотрим поиск в ширину.
