На этом шаге мы приведем реализацию этого алгоритма.

    Чтобы перейти от поиска BFS к поиску А*, нужно внести в код пару незначительных изменений. Прежде всего изменить область поиска с очереди на очередь с приоритетом. Таким образом, в области поиска появятся узлы с наименьшим f(n). Затем нужно заменить исследуемый набор на словарь. Он позволит отслеживать наименьшие затраты (g(n)) для каждого узла, который мы можем посетить. Теперь, когда используется эвристическая функция, может оказаться, что некоторые узлы будут проверены дважды, если эвристика окажется несовместимой. Если узел, найденный в новом направлении, требует меньших затрат, чем тогда, когда мы его посетили в прошлый раз, то мы предпочтем новый маршрут.

    Для простоты функция astar() не принимает в качестве параметра функцию вычисления затрат. Вместо этого мы считаем, что затраты для каждого шага в лабиринте равны 1. Каждому новому узлу назначаются затраты, основанные на этой простой формуле, а также эвристический показатель, вычисленный с использованием новой функции heuristic(), передаваемой функции поиска в качестве параметра. За исключением этих изменений, функция astar() очень похожа на bfs() (файл generic_search.py).

def astar(initial: T, goal_test: Callable[[T], bool],
          successors: Callable[[T], List[T]],
          heuristic: Callable[[T], float]) -> Optional[Node[T]]:
    # froпtier - то, куда мы хотим двигаться
    frontier: PriorityQueue[Node[T]] = PriorityQueue()
    frontier.push(Node(initial, None, 0.0, heuristic(initial)))
    # expLored - то, что мы уже просмотрели
    explored: Dict[T, float] = {initial: 0.0}
    # продолжаем, пока есть что просматривать
    while not frontier.empty:
        current_node: Node[T] = frontier.pop()
        current_state: T = current_node.state
        # если цель найдена, мы закончили
        if goal_test(current_state):
            return current_node
        # проверяем, в какую из неисследованных ячеек направиться
        for child in successors(current_state):
            new_cost: float = current_node.cost + 1
            # 1 - для сетки, для более сложных приложений здесь
            # должна быть функция затрат

            if child not in explored or explored[child] > new_cost:
                explored[child] = new_cost
                frontier.push(Node(child, current_node, new_cost, heuristic(child)))
    return None # все проверили, пути к целевой точке не нашли

    Поздравляем! Если вы завершили этот путь, то узнали не только о том, как пройти по лабиринту, но и о некоторых общих функциях поиска, которые сможете использовать во всевозможных поисковых приложениях. Алгоритмы DFS и BFS подходят для множества небольших наборов данных и пространств состояний, где производительность не очень важна. В некоторых ситуациях DFS превосходит BFS, но преимущество BFS заключается в том, что этот алгоритм всегда гарантирует оптимальный путь. Интересно, что у BFS и DFS почти идентичные реализации, различающиеся только применением очереди вместо стека в качестве области поиска. Чуть более сложный поиск А* в сочетании с хорошей последовательной допустимой эвристикой не только обеспечивает оптимальный путь, но и намного превосходит BFS по производительности. А поскольку все три функции были реализованы в параметризованном виде, их можно использовать практически в любом пространстве поиска - достаточно просто написать

import generic_search                         .

    Вперед - попробуйте применить astar() к тому же лабиринту.

if __name__ == "__main__":
    # Тестирование DFS
    m: Maze = Maze()
    print(m)
    solution1: Optional[Node[MazeLocation]] = dfs(m.start, m.goal_test, m.successors)
    if solution1 is None:
        print("Поиском в глубину решение не найдено!")
    else:
        path1: List[MazeLocation] = node_to_path(solution1)
        m.mark(path1)
        print(m)
        m.clear(path1)
    # Тестирование BFS
    solution2: Optional[Node[MazeLocation]] = bfs(m.start, m.goal_test, m.successors)
    if solution2 is None:
        print("Поиском в ширину решение не найдено!")
    else:
        path2: List[MazeLocation] = node_to_path(solution2)
        m.mark(path2)
        print(m)
        m.clear(path2)
    # Тестирование А*
    distance: Callable[[MazeLocation], float] = manhattan_distance(m.goal)
    solutionЗ: Optional[Node[MazeLocation]] = astar(m.start, m.goal_test, 
                                m.successors, distance)
    if solutionЗ is None:
        print("Алгоритмом А* решение не найдено!")
    else:
        pathЗ: List[MazeLocation] = node_to_path(solutionЗ)
        m.mark(pathЗ)
        print(m)

    Интересно, что результат немного отличается от bfs(), несмотря на то что и bfs(), и astar() находят оптимальные (равные по длине) пути. Из-за своей эвристики astar() сразу проходит по диагонали к цели. В итоге этот алгоритм проверяет меньше состояний, чем bfs(), что обеспечивает более высокую производительность. Если хотите в этом убедиться, добавьте счетчик состояний для каждого алгоритма:

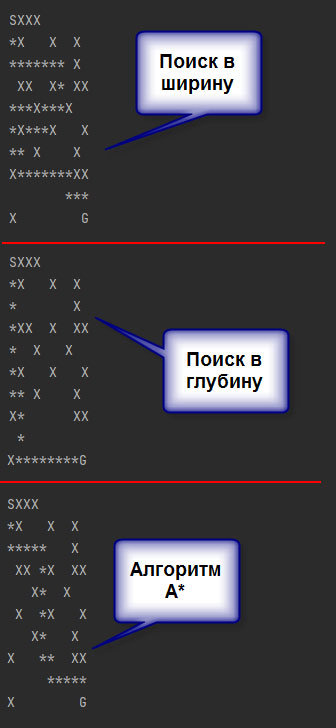
Рис.1. Результат работы приложения

    Со следующего шага мы начнем рассмотривать задачу про миссионеров и людоедов.

Предыдущий шаг Содержание Следующий шаг