На этом шаге мы рассмотрим решение этой задачи.

    Представьте, что у вас есть карта Австралии, на которой вы хотите разными цветами обозначить штаты/территории (мы будем называть те и другие регионами). Никакие две соседние области не должны быть окрашены в одинаковый цвет. Можно ли раскрасить регионы всего тремя разными цветами?

    Ответ: да. Попробуйте сами (самый простой способ - напечатать карту Австралии с белым фоном). Мы, люди, можем быстро найти решение путем изучения карты и небольшого количества проб и ошибок. На самом деле это тривиальная задача, которая отлично подойдет в качестве первой для нашей программы решения задач с ограничениями методом поиска с возвратом (рисунок 1).

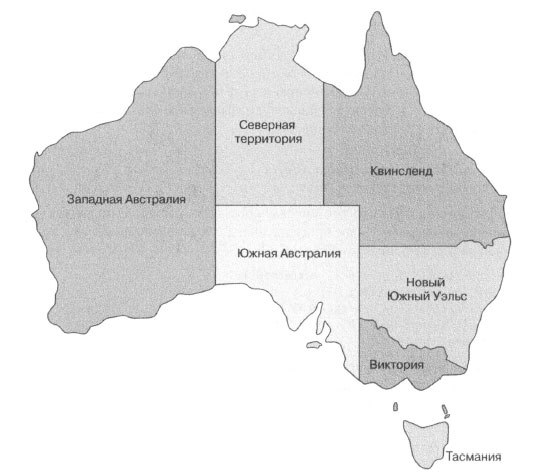
Рис.1. В решении задачи раскраски карты Австралии никакие две смежные ее части не могут быть окрашены в один и тот же цвет

    Чтобы смоделировать проблему как CSP, нужно определить переменные, области определения и ограничения. Переменными являются семь регионов Австралии (по крайней мере те семь, которыми мы ограничимся):

• Западная Австралия,
• Северная территория,
• Южная Австралия,
• Квинсленд,
• Новый Южный Уэльс,
• Виктория и
• Тасмания.

    В нашем CSP их можно представить как строки. Область определения каждой переменной - это три разных цвета, которые могут быть ей присвоены. (Мы используем красный, зеленый и синий.) Ограничения - сложный вопрос. Никакие две соседние области не могут быть окрашены в один и тот же цвет, поэтому ограничения будут зависеть от того, какие области граничат друг с другом. Мы задействуем так называемые двоичные ограничения - ограничения между двумя переменными. Каждые две области с общей границей будут иметь двоичное ограничение, указывающее, что им нельзя присвоить один и тот же цвет.

    Чтобы реализовать такие двоичные ограничения в коде, нужно создать подкласс класса Constraint. Конструктор подкласса MapColoringConstraint будет принимать две переменные - две области, имеющие общую границу. Его переопределенный метод satisfied() сначала проверит, присвоены ли этим двум областям значения (цвета) из области определения. Если нет, то ограничение считается тривиально выполненным до тех пор, пока цвета не будут присвоены. (Пока у одного из регионов нет цвета, конфликт невозможен.) Затем метод проверит, присвоен ли двум областям один и тот же цвет. Очевидно, что если цвета одинаковы, то существует конфликт, означающий: ограничение не выполняется.

    Далее этот класс представлен во всей своей полноте. Сам по себе класс MapColoringConstraint не универсален с точки зрения аннотации типа, но он является подклассом параметризованной версии универсального класса Constraint, которая указывает, что переменные и области определения имеют тип str.

from csp import Constraint, CSP
from typing import Dict, List, Optional


class MapColoringConstraint(Constraint[str, str]):
    def __init__(self, place1: str, place2: str) -> None:
        super().__init__([place1, place2])
        self.place1: str = place1
        self.place2: str = place2

    def satisfied(self, assignment: Dict[str, str]) -> bool:
        # если какой-либо регион place отсутствует в присваивании,
        # то его цвета не могут привести к конфликту
        if self.place1 not in assignment or self.place2 not in assignment:
            return True
        # проверяем, не совпадает ли цвет, присвоенный pLace1,
        # с цветом, присвоенным place2
        return assignment[self.place1] != assignment[self.place2]

Для вызова метода суперкласса иногда используется метод super(), но можно взять и имя самого класса, как в Constraint.__init__([placel, place2]). Это особенно полезно во время работы с множественным наследованием, так как позволяет знать, какой именно метод суперкласса вы вызываете.

    Теперь, когда есть способ реализации ограничений между регионами, можно легко уточнить задачу о раскраске карты Австралии с помощью программы решения методом CSP - нужно лишь заполнить области определения и переменные, а затем добавить ограничения.

if __name__ == "__main__":
    variables: List[str] = ["Западная Австралия", "Северная территория", "Южная Австралия",
                            "Квинсленд", "Новый Южный Уэльс", "Виктория", "Тасмания"]
    domains: Dict[str, List[str]] = {}
    for variable in variables:
        domains[variable] = ["красный", "зеленый", "синий"]
    csp: CSP[str, str] = CSP(variables, domains)
    csp.add_constraint(MapColoringConstraint("Западная Австралия", "Северная территория"))
    csp.add_constraint(MapColoringConstraint("Западная Австралия", "Южная Австралия"))
    csp.add_constraint(MapColoringConstraint("Южная Австралия", "Северная территория"))
    csp.add_constraint(MapColoringConstraint("Квинсленд", "Северная территория"))
    csp.add_constraint(MapColoringConstraint("Квинсленд", "Южная Австралия"))
    csp.add_constraint(MapColoringConstraint("Квинсленд", "Новый Южный Уэльс"))
    csp.add_constraint(MapColoringConstraint("Новый Южный Уэльс", "Южная Австралия"))
    csp.add_constraint(MapColoringConstraint("Виктория", "Южная Австралия"))
    csp.add_constraint(MapColoringConstraint("Виктория", "Новый Южный Уэльс"))
    csp.add_constraint(MapColoringConstraint("Виктория", "Тасмания"))

    Наконец, вызываем backtracking_search() для поиска решения.

    solution: Optional[Dict[str, str]] = csp.backtracking_search()
    if solution is None:
        print("Решение не найдено!")
    else:
        print(solution)

    Правильное решение будет представлять собой список цветов, присвоенных регионам:

{'Западная Австралия': 'красный', 'Северная территория': 'зеленый', 
'Южная Австралия': 'синий', 'Квинсленд': 'красный', 
'Новый Южный Уэльс': 'зеленый', 'Виктория': 'красный', 
'Тасмания': 'зеленый'}

    На следующем шаге мы рассмотрим задачу восьми ферзей.

Предыдущий шаг Содержание Следующий шаг