На этом шаге мы представим карту в виде графа.
В этом и следующих шагах мы будем работать не с графом станций метро, а с городами Соединенных Штатов Америки и возможными маршрутами между ними. На рисунке 1 представлена карта континентальной части США с 15 крупнейшими муниципальными статистическими районами (Metropolitan Statistical Area, MSA) страны, согласно оценкам Бюро переписи США.
Данные предоставлены американским Бюро переписи США (American Fact Finder).
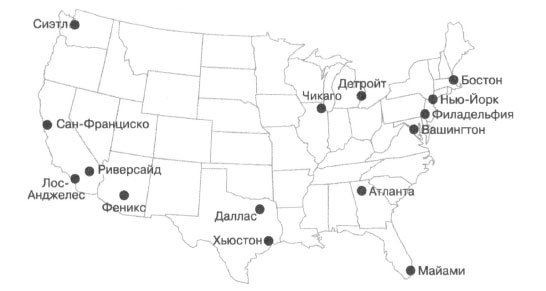
Рис.1. Карта 15 крупнейших муниципальных статистических районов США
Известный предприниматель Илон Маск предложил построить высокоскоростную транспортную сеть, состоящую из капсул, перемещающихся в герметичных трубах. Маек утверждает, что капсулы будут передвигаться со скоростью 700 миль в час и позволят создать экономически эффективный междугородный транспорт для расстояний до 900 миль. Маск называет эту новую транспортную систему Hyperloop. Здесь мы рассмотрим классические графовые задачи в контексте построения такой транспортной сети.
Сначала Маск предложил идею Hyperloop для соединения Лос-Анджелеса и Сан-Франциско. Если бы потребовалось построить национальную сеть Hyperloop, то было бы целесообразно соединить крупнейшие мегаполисы Америки. На рисунке 2 удалены границы штатов, которые были обозначены на рисунке 1. Кроме того, каждый муниципальный статистический район связан с несколькими соседними. Это соседи не всегда являются ближайшими соседними MSA что делает граф намного интереснее..
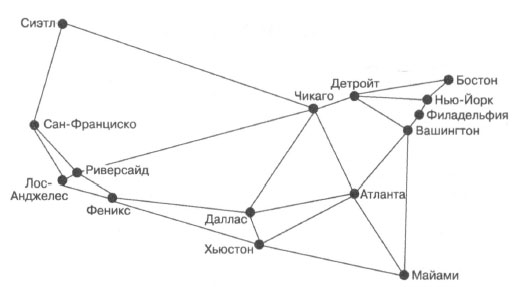
Рис.2. Граф, в котором вершины представляют 15 крупнейших муниципальных статистических районов США, а ребра - потенциальные маршруты Hyperloop между ними
На рисунке 2 показан граф с вершинами, соответствующими 15 крупнейшим MSA Соединенных Штатов, и ребрами, обозначающими потенциальные маршруты Hyperloop между городами. Маршруты были выбраны в иллюстративных целях. Конечно, в состав сети Hyperloop могут входить и другие потенциальные маршруты.
Такое абстрактное представление реальной задачи подчеркивает эффективность графов. Благодаря этой абстракции можно игнорировать географию Соединенных Штатов и сосредоточиться на изучении потенциальной сети Hyperloop только в контексте соединения городов. В сущности, мы можем представить задачу в виде любого графа, если только его ребра остаются неизменными. Например, на рисунке 3 изменено положение Майами. Граф, изображенный здесь, будучи абстрактным представлением, позволяет решать те же фундаментальные вычислительные задачи, что и граф на рисунке 2, несмотря на то что Майами на нем находится не там, где мы ожидаем. Но из соображений здравого смысла будем придерживаться представления, приведенного на рисунке 2.
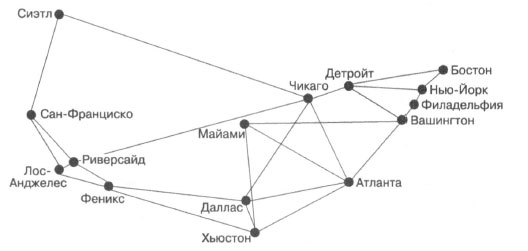
Рис.3. График, эквивалентный показанному на рисунке 2, с измененным положением Майами
На следующем шаге мы рассмотрим построение графовой структуры.
