На этом шаге мы рассмотрим применимость этого алгоритма к решению задачи поиска крадчайшего пути.
В невзвешенном графе поиск кратчайшего пути означает поиск пути с наименьшим количеством ребер между начальной и конечной вершинами. При построении сети Hyperloop, возможно, имеет смысл сначала подключить самые отдаленные города на густонаселенных побережьях. Возникает вопрос: какой путь между Бостоном и Майами является кратчайшим?
К счастью, у нас уже есть алгоритм поиска кратчайших путей, и с его помощью мы можем ответить на этот вопрос. Поиск в ширину, описанный на 27 шаге, подходит для графов так же, как и для лабиринтов. В сущности, лабиринты, с которыми мы работали, на самом деле являются графами. Вершины - это точки лабиринта, а ребра - ходы, которые можно сделать, чтобы попасть из одной точки в другую. В невзвешенном графе поиск в ширину найдет кратчайший путь между любыми двумя вершинами.
Мы можем повторно использовать реализацию поиска в ширину для работы с Graph. Да что там, ее можно применить вообще без изменений. Вот что значит параметризованный код!
Напомним, что функции bfs(), описанной на 29 шаге, требуются три параметра:
- начальное состояние,
- Callable (объект, похожий на функцию чтения) для проверки того, достигнута ли цель, и
- Callable для поиска состояний - наследников данного состояния.
Учитывая этот план, мы можем добавить соответствующий код в конец основного раздела последнего приложения, чтобы найти на city_graph кратчайший маршрут между Бостоном и Майами.
. . . . from generic_search import bfs, Node, node_to_path . . . . bfs_result: Optional[Node[V]] = bfs("Бостон", lambda х: х == "Майами", city_graph.neighbors_for_vertex) if bfs_result is None: print("Решение не найдено с помощью поиска в ширину!") else: path: List[V] = node_to_path(bfs_result) print("Путь от Бостона до Майами:") print(path)
Результат должен выглядеть примерно так:
Путь от Бостона до Майами: ['Бостон', 'Детройт', 'Вашингтон', 'Майами']
Путь Бостон - Детройт - Вашингтон - Майами, состоящий из трех ребер, - это самый короткий маршрут между Бостоном и Майами с точки зрения количества ребер (рисунок 1).
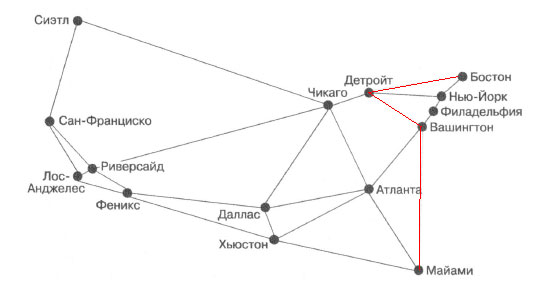
Рис.1. Здесь выделен кратчайший маршрут между Бостоном и Майами с точки зрения количества ребер
На следующем шаге мы рассмотрим минимизацию затрат на построение сети.
