На этом шаге мы рассмотрим алгоритм Ярника.
Алгоритм Ярника для поиска минимального связующего (остовного) дерева решает задачу посредством деления графа на две части: вершины в формируемом минимальном связующем дереве и вершины, еще не входящие в минимальное связующее дерево. Алгоритм выполняет следующие шаги.
- Выбрать произвольную вершину для включения в минимальное связующее дерево.
- Найти ребро с наименьшим весом, соединяющее минимальное связующее дерево с вершинами, еще не входящими в минимальное связующее дерево.
- Добавить вершину, расположенную на конце этого минимального ребра, к минимальному связующему дереву.
- Повторять шаги 2 и 3, пока все вершины графа не будут включены в минимальное связующее дерево.
Алгоритм Ярника часто называют алгоритмом Прима. Два чешских математика, Отакар Борувка и Войцех Ярник, заинтересовавшись минимизацией затрат на
прокладку электрических линий в конце 1920-х годов, придумали алгоритмы для решения задачи поиска минимального связующего дерева.
Их алгоритмы были "переоткрыты" другими учеными несколько десятков лет спустя (Durnova Н. Otakar Boruvka (1899-1995) and the Miniшшn Spanning Tree. -
Institute of Matheшatics of the Czech Асаdешу at· Sciences, 2006.).
Для эффективного выполнения алгоритма Ярника используется очередь с приоритетом. Каждый раз, когда новая вершина добавляется в минимальное связующее дерево, все ее исходящие ребра, которые связываются с вершинами вне дерева, добавляются в очередь с приоритетом. Ребро с наименьшим весом всегда первым извлекается из очереди с приоритетом, и алгоритм продолжает выполняться до тех пор, пока очередь с приоритетом не опустеет. Это гарантирует, что ребра с наименьшим весом всегда будут первыми добавляться в дерево. Ребра, которые соединяются с вершинами, уже находящимися в дереве, игнорируются при извлечении из очереди. Далее представлены код функции mst() - полная реализация алгоритма Ярника (Седжвик Р., .Уэйн К. Алгоритмы нa.Java. 4-е изд. - М.: Вильяме, 2013.), а также вспомогательная функция для печати WeightedPath.
Алгоритм Ярника не всегда правильно работает для графов с направленными ребрами. Он не подействует и для несвязных графов.
def mst(wg: WeightedGraph[V], start: int = 0) -> Optional[WeightedPath]: if start > (wg.vertex_count - 1) or start < 0: return None result: WeightedPath = [] # содержит окончательное MST pq: PriorityQueue[WeightedEdge] = PriorityQueue() visited: [bool] = [False] * wg.vertex_count # здесь мы уже были def visit(index: int): visited[index] = True # пометить как прочитанное for edge in wg.edges_for_index(index): # добавляем вВсе ребра отсюда в pq if not visited[edge.v]: pq.push(edge) visit(start) # первая вершина, с которой все начинается while not pq.empty: # продолжаем, пока остаются необработанные вершины edge = pq.pop() if visited[edge.v]: continue # никогда не просматриваем дважды # на данный момент это минимальный вес, так что добавляем в дерево result.append(edge) visit(edge.v) return result def print_weighted_path(wg: WeightedGraph, wp: WeightedPath) -> None: for edge in wp: print(f"{wg.vertex_at(edge.u)} {edge.weight}> {wg.vertex_at(edge.v)}") print(f"Общая длина: {total_weight(wp)}")
Алгоритм возвращает необязательный объект WeightedPath, представляющий собой минимальное связующее (остовное) дерево. Не имеет значения, с какой вершины начинается алгоритм (при условии, что граф является связным и ненаправленным), поэтому по умолчанию выбирается начальная вершина с индексом 0. Если значение start оказалось неверным, то mst() возвращает None.
result: WeightedPath = [] # содержит окончательное MST
pq: PriorityQueue[WeightedEdge] = PriorityQueue()
visited: [bool] = [False] * wg.vertex_count # здесь мы уже были
В итоге result будет содержать взвешенный путь, куда входит минимальное связующее дерево. Именно здесь добавляются объекты WeightedEdge, так как ребро с наименьшим весом извлекается из очереди и переводит нас к новой части графа. Алгоритм Ярника считается жадным алгоритмом, потому что всегда выбирает ребро с наименьшим весом. В pq хранятся новые обнаруженные ребра, и отсюда извлекается следующее ребро с наименьшим весом. В visited отслеживаются индексы вершин, которые мы уже просмотрели. Это можно сделать также с помощью Set, аналогичного explored в bfs():
def visit(index: int):
visited[index] = True # пометить как прочитанное
for edge in wg.edges_for_index(index):
# добавляем вВсе ребра отсюда в pq
if not visited[edge.v]:
pq.push(edge)
visit() - это внутренняя вспомогательная функция, которая отмечает вершину как просмотренную и добавляет в pq все ее ребра, которые соединяются с еще не просмотренными вершинами. Обратите внимание на то, как легко модель списка смежности облегчает поиск ребер, принадлежащих определенной вершине:
visit(start) # первая вершина, с которой все начинается
Если граф несвязный, то не имеет значения, какая вершина рассматривается первой. Если несвязный граф состоит из разъединенных компонентов, то mst() вернет дерево, охватывающее тот компонент, которому принадлежит начальная вершина:
while not pq.empty: # продолжаем, пока остаются необработанные вершины
edge = pq.pop()
if visited[edge.v]:
continue # никогда не просматриваем дважды
# на данный момент это минимальный вес, так что добавляем в дерево
result.append(edge)
visit(edge.v)
return result
Пока в очереди с приоритетом остаются ребра, мы извлекаем их оттуда и проверяем, ведут ли они к вершинам, которых еще нет в дереве. Поскольку очередь с приоритетом является возрастающей, из нее сначала извлекаются ребра с наименьшим весом. Это гарантирует, что результат действительно имеет минимальный общий вес. Если ребро, извлеченное из очереди, не приводит к неисследованной вершине, то оно игнорируется. В противном случае, поскольку ребро имеет минимальный из всех видимых весов, оно добавляется к результирующему набору и исследуется новая вершина, к которой ведет это ребро. Когда неисследованных ребер не остается, возвращается результат.
Теперь мы наконец вернемся к задаче соединения всех 15 крупнейших MSA Соединенных Штатов в сеть Hyperloop минимальным количеством трасс. Маршрут, выполняющий эту задачу, является просто минимальным связующим деревом для city_graph2. Попробуем запустить mst() для city_graph2.
if __name__ == "__main__": city_graph2: WeightedGraph[str] = WeightedGraph(["Сиэтл", "Сан-Франциско", "Лос-Анджелес", "Риверсайд", "Феникс", "Чикаго", "Бостон", "Нью-Йорк", "Атланта", "Майами", "Даллас", "Хьюстон", "Детройт", "Филадельфия", "Вашингтон"]) city_graph2.add_edge_by_vertices("Сиэтл", "Чикаго", 1737) city_graph2.add_edge_by_vertices("Сиэтл", "Сан-Франциско", 678) city_graph2.add_edge_by_vertices("Сан-Франциско", "Риверсайд", 386) city_graph2.add_edge_by_vertices("Сан-Франциско", "Лос-Анджелес", 348) city_graph2.add_edge_by_vertices("Лос-Анджелес", "Риверсайд", 50) city_graph2.add_edge_by_vertices("Лос-Анджелес", "Феникс", 357) city_graph2.add_edge_by_vertices("Риверсайд", "Феникс", 307) city_graph2.add_edge_by_vertices("Риверсайд", "Чикаго", 1704) city_graph2.add_edge_by_vertices("Феникс", "Даллас", 887) city_graph2.add_edge_by_vertices("Феникс", "Хьюстон", 1015) city_graph2.add_edge_by_vertices("Даллас", "Чикаго", 805) city_graph2.add_edge_by_vertices("Даллас", "Атланта", 721) city_graph2.add_edge_by_vertices("Даллас", "Хьюстон", 225) city_graph2.add_edge_by_vertices("Хьюстон", "Атланта", 702) city_graph2.add_edge_by_vertices("Хьюстон", "Майами", 968) city_graph2.add_edge_by_vertices("Атланта", "Чикаго", 588) city_graph2.add_edge_by_vertices("Атланта", "Вашингтон", 543) city_graph2.add_edge_by_vertices("Атланта", "Майами", 604) city_graph2.add_edge_by_vertices("Майами", "Вашингтон", 923) city_graph2.add_edge_by_vertices("Чикаго", "Детройт", 238) city_graph2.add_edge_by_vertices("Детройт", "Бостон", 613) city_graph2.add_edge_by_vertices("Детройт", "Вашингтон", 396) city_graph2.add_edge_by_vertices("Детройт", "Нью-Йорк", 482) city_graph2.add_edge_by_vertices("Бостон", "Нью-Йорк", 190) city_graph2.add_edge_by_vertices("Нью-Йорк", "Филадельфия", 81) city_graph2.add_edge_by_vertices("Филадельфия", "Вашингтон", 123) result: Optional[WeightedPath] = mst(city_graph2) if result is None: print("Решение не найдено!") else: print_weighted_path(city_graph2, result)
Благодаря методу структурной печати printWeightedPath() минимальное связующее дерево легко читается:
Сиэтл 678> Сан-Франциско Сан-Франциско 348> Лос-Анджелес Лос-Анджелес 50> Риверсайд Риверсайд 307> Феникс Феникс 887> Даллас Даллас 225> Хьюстон Хьюстон 702> Атланта Атланта 543> Вашингтон Вашингтон 123> Филадельфия Филадельфия 81> Нью-Йорк Нью-Йорк 190> Бостон Вашингтон 396> Детройт Детройт 238> Чикаго Атланта 604> Майами Общая длина: 5372
Другими словами, это суммарно кратчайший набор ребер, который соединяет все MSA во взвешенном графе. Минимальная длина трассы, необходимой для соединения всех ребер, составляет 5372 мили. Минимальное связующее дерево показано на рисунке 1.
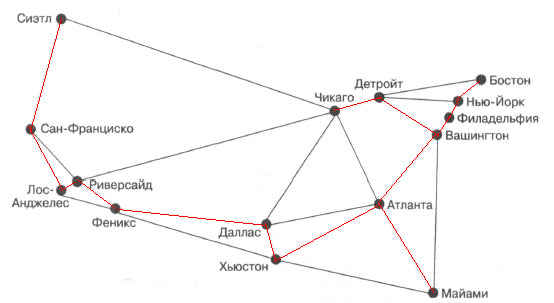
Рис.1. Выделенные красным цветом ребра образуют минимальное связующее дерево, которое соединяет все 15 MSA
На следующем шаге мы рассмотрим поиск кратчайших путей во взвешенном графе.
