На этом шаге мы закончим построение генетического алгоритма.
Теперь рассмотрим два метода отбора, которые поддерживает наш класс.
# Используем метод рулетки с нормальным распределением,
# чтобы выбрать двух родителей
# Примечание: не работает при отрицательных значениях жизнеспособности
def _pick_roulette(self, wheel: List[float]) -> Tuple[C, C]:
return tuple(choices(self._population, weights=wheel, k=2))
Выбор метода рулетки основан на отношении жизнеспособности каждой хромосомы к суммарной жизнеспособности всех хромосом данного поколения. Хромосомы с самой высокой жизнеспособностью имеют больше шансов быть отобранными. Значения, которые соответствуют жизнеспособности хромосомы, указаны в параметре wheel. Реальный выбор удобно выполнять с помощью функции choices() из модуля random стандартной библиотеки Python. Эта функция принимает список элементов, из которых мы хотим сделать выбор, список такой же длины, содержащий веса всех элементов первого списка, и число выбираемых элементов.
Если бы мы реализовывали это сами, то могли бы рассчитать в процентах долю от общей жизнеспособности для каждого элемента (пропорциональной жизнеспособности), представленную значениями с плавающей запятой от 0 до 1. Случайное число (pick) от 0 до 1 можно использовать для вычисления того, какую хромосому отобрать. Алгоритм будет работать, последовательно уменьшая pick на величину пропорциональной жизнеспособности каждой хромосомы. Когда pick станет меньше 0, это и будет хромосома для отбора.
Понимаете ли вы, почему этот процесс приводит к тому, что каждая хромосома выбирается по ее пропорциональной жизнеспособности? Если нет, подумайте об этом с карандашом и бумагой. Попробуйте нарисовать метод пропорционального отбора, как показано на рисунке 1.
Простейшая форма турнирного отбора проще, чем отбор методом рулетки. Вместо того чтобы вычислять пропорции, мы просто выбираем случайным образом k хромосом из всей популяции. В отборе побеждают две хромосомы с наилучшей жизнеспособностью из случайно выбранной группы:
# Выбираем случайным образом пиm_participaпts и берем из них две лучших
def _pick_tournament(self, num_participants: int) -> Tuple[C, C]:
participants: List[C] = choices(self._population, k=num_participants)
return tuple(nlargest(2, participants, key=self._fitness_key))
В коде для _pick_tournament() вначале используется choices(), чтобы случайным образом выбрать num_participants из _population. Затем с помощью функции nlargest() из модуля heapq находим двух самых больших индивидуумов по _fitness_key. Каково правильное количество для num_participants? Как и во многих других параметрах генетического алгоритма, наилучшим способом определения этого значения может быть метод проб и ошибок. Следует иметь в виду, что чем больше участников турнира, тем меньше разнообразие в популяции, потому что хромосомы с плохой жизнеспособностью с большей вероятностью будут устранены в процессе поединков между особями.
 Sokolov Л., Whitley D. Unbiased Tournament Selection // GECCO'05. - June 25-29. Washington, D. C., U.S.A., 2005.
Sokolov Л., Whitley D. Unbiased Tournament Selection // GECCO'05. - June 25-29. Washington, D. C., U.S.A., 2005.
Более сложные формы турнирного отбора могут выбирать особей, которые являются не самыми лучшими, а лишь вторыми или третьими по жизнеспособности, основываясь на некоторой модели убывающей вероятности.
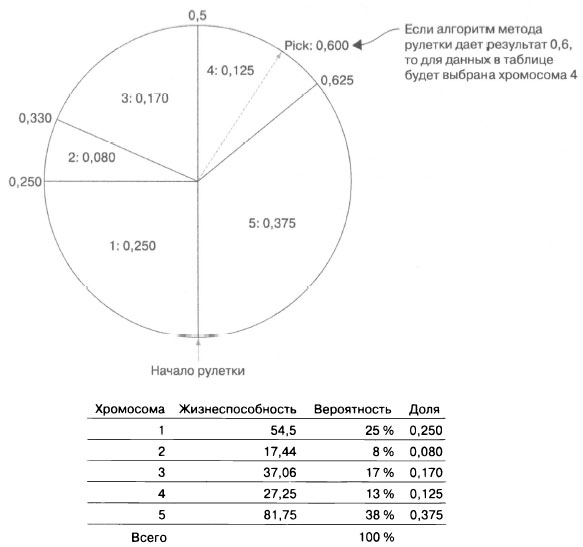
Рис.1. Пример отбора методом рулетки
Методы _pick_roulette() и _pick_tournament() используются для отбора, выполняемого в процессе размножения. Воспроизводство реализовано в методе _reproduce_and_replace(), который заботится о том, чтобы на смену хромосомам последнего поколения пришла новая популяция с тем же количеством хромосом:
# Замена популяции новым поколением особей
def _reproduce_and_replace(self) -> None :
new_population: List[C] = []
# продолжаем, пока не заполним особями все новое поколение
while len(new_population) < len(self._population):
# выбор двух родителей
if self._selection_type == GeneticAlgorithm.SelectionType.ROULETTE:
parents: Tuple[C, C] = self._pick_roulette(
[x.fitness() for x in self._population])
else:
parents = self._pick_tournament(len(self._population) // 2)
# потенциальное скрещивание двух родителей
if random() < self._crossover_chance:
new_population.extend(parents[0].crossover(parents[1]))
else:
new_population.extend(parents)
# если число нечетное, то один лишний, поэтому удаляем его
if len(new_population) > len(self._population):
new_population.pop()
self._population = new_population # заменяем ссылку
В _reproduce_and_replace() выполняются следующие основные операции.
- Две хромосомы, называемые родителями (parents), отбираются для воспроизводства посредством одного из двух методов отбора. При турнирном отборе всегда проводится
турнир среди половины популяции, но этот способ можно настраивать в конфигурации.
- Существует вероятность _crossover_chance того, что для получения двух новых хромосом два родителя будут объединены. В этом случае они добавляются в новую популяцию
(new_population). Если потомков нет, то два родителя просто добавляются в new_population.
- Если новая популяция new_population содержит столько же хромосом, сколько и старая _population, то она ее заменяет. В противном случае возвращаемся к шагу 1.
Метод _mutate(), который реализует мутацию, очень прост, подробная реализация мутации предоставляется отдельным хромосомам:
# Каждая особь мутирует с вероятностью _mutation_chance
def _mutate(self) -> None :
for individual in self._population:
if random() < self._mutation_chance:
individual.mutate()
Теперь у нас есть все строительные блоки, необходимые для запуска генетического алгоритма. Метод run() координирует этапы измерений, воспроизводства (включая отбор) и мутации, в процессе которых одно поколение популяции заменяется другим. Этот метод также отслеживает лучшие, наиболее жизнеспособные хромосомы, обнаруженные на любом этапе поиска:
# Выполнение генетического алгоритма для max_generations итераций
# и возвращение лучшей из найденных особей
def run(self) -> C:
best: C = max(self._population, key=self._fitness_key)
for generation in range(self._max_generations):
# ранний выход, если превышен порог
if best.fitness() >= self._threshold:
return best
print(f"Генерация {generation} Лучшая {best.fitness()} "
f"Среднее {mean(map(self._fitness_key, self._population))}")
self._reproduce_and_replace()
self._mutate()
highest: C = max(self._population, key=self._fitness_key)
if highest.fitness() > best.fitness():
best = highest # найден новый лучший результат
return best # лучший найденный результат из max_generations
Значение best позволяет отслеживать лучшую из найденных до сих пор хромосом. Основной цикл выполняется _max_generations раз. Если какая-либо хромосома превышает порог жизнеспособности, то она возвращается и метод заканчивается. В противном случае метод вызывает _reproduce_and_replace() и _mutate() для создания следующего поколения и повторного запуска цикла. Если достигается значение _max_generations, то возвращается лучшая хромосома из найденных до сих пор.
На следующем шаге мы протестируем созданный алгоритм.
