На этом шаге мы рассмотрим создание этого алгоритма.
Метод k-средних - это алгоритм кластеризации, который стремится сгруппировать единицы данных в некое заранее определенное количество кластеров, основываясь на относительном расстоянии от центра кластера до каждой единицы. В каждом периоде k-средних вычисляется расстояние между каждой единицей данных и каждым центром кластера - единицей данных, известной как центроид. Единицы данных присваиваются кластеру, к центроиду которого они ближе всего. Затем алгоритм пересчитывает все центроиды, находя среднее значение единиц данных, назначенных каждому кластеру, и заменяя старый центроид новым средним. Процесс назначения единиц данных и пересчета центроидов продолжается до тех пор, пока центроиды не перестанут передвигаться или не будет выполнено определенное количество итераций.
Все измерения начальных точек, представленных k-средними, должны быть сопоставимыми по величине. Иначе k-средние будут отклоняться в сторону кластеризации на основе измерений с наибольшим отличием. Процесс сопоставления разных типов данных (в нашем случае разных измерений) называется нормализацией. Одним из распространенных способов нормализации данных является приближенная оценка каждого значения на основе его z-оценки, известной также как стандартная оценка, относительно других значений того же типа. Z-оценка рассчитывается путем вычитания среднего всех значений из данного значения и деления результата на стандартное отклонение всех значений. Функция zscores(), разработанная в начале предыдущего шага, делает именно это для каждого значения итерируемого объекта, состоящего из значений типа float.
Основная сложность, связанная с алгоритмом k-средних, заключается в определении способа выбора начальных центроидов. В простейшей форме алгоритма, которую мы будем реализовывать, начальные центроиды размещаются случайным образом в пределах диапазона данных. Сложно также решить, на сколько кластеров разделить данные (k в k-средних). В классическом алгоритме это число определяет пользователь, но он может не знать правильного числа, и его определение потребует некоторого количества экспериментов. Мы позволим пользователю определить k.
Объединяя все эти этапы и соображения, получим следующий алгоритм кластеризации методом k-средних.
- Инициализировать все единицы данных и k пустых кластеров.
- Нормализовать все единицы данных.
- Создать случайные центроиды, связанные с каждым кластером.
- Назначить каждую единицу данных кластеру того центроида, к которому она расположена ближе всего.
- Пересчитать каждый центроид, чтобы он был центром (средним) кластера, с которым связан.
- Повторять пункты 4 и 5, пока не будет выполнено максимально допустимое количество итераций или пока центроиды не перестанут передвигаться (сходиться).
Концептуально метод k-средних, в сущности, очень прост: на каждой итерации каждая единица данных связана с тем кластером, к центру которого она расположена ближе всего. По мере того как в кластер вносятся новые единицы данных, этот центр перемещается (рисунок 1).
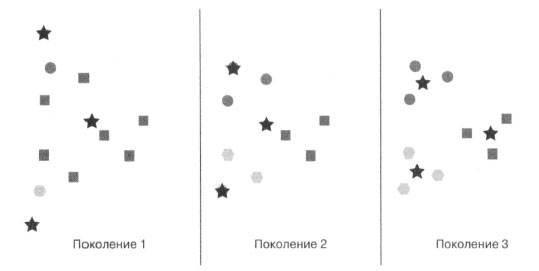
Рис.1. Пример метода k-средних, выполняемого на протяжении трех поколений для произвольного набора данных. Звездочками отмечены центроиды. Оттенком и формой обозначено текущее членство в кластере (оно изменяется)
Далее реализован класс для поддержания состояния и выполнения алгоритма, аналогичный GeneticAlgorithm, описанному на 65 шаге. Теперь мы вернемся к файлу, где реализована функция zscores().
Point = TypeVar('Point', bound=DataPoint) class KMeans(Generic[Point]): @dataclass class Cluster: points: List[Point] centroid: DataPoint
KMeans - это параметризованный класс. Он работает с DataPoint или с любым подклассом DataPoint, как определено значением bound типа Point. У него есть внутренний класс Cluster, который отслеживает отдельные кластеры в процессе выполнения операции. У каждого Cluster есть связанные с ним единицы данных и центроид.
Теперь определим метод __init__() для внешнего класса:
def __init__(self, k: int, points: List[Point]) -> None :
if k < 1: # Число кластеров, создаваемых методом k-средних,
# не может быть отрицательным или равным нулю
raise ValueError("k должно быть >= 1")
self._points: List[Point] = points
self._zscore_normalize()
# инициализируем пустые кластеры случайными центроидами
self._clusters: List[KMeans.Cluster] = []
for _ in range(k):
rand_point: DataPoint = self._random_point()
cluster: KMeans.Cluster = KMeans.Cluster([], rand_point)
self._clusters.append(cluster)
@property
def _centroids(self) -> List[DataPoint]:
return [x.centroid for x in self._clusters]
С классом KMeans связан массив _points. Это все единицы данных из набора данных. Затем единицы данных делятся между кластерами, которые хранятся в соответствующей переменной _clusters. Когда создается экземпляр KMeans, он должен знать, сколько кластеров требуется создать (k). Каждый кластер изначально имеет случайный центроид. Все единицы данных, которые будут использоваться в алгоритме, нормализуются по z-оценке. Вычисляемое свойство _centroids возвращает все центроиды, связанные с кластерами, создаваемыми алгоритмом:
def _dimension_slice(self, dimension: int) -> List[float]:
return [x.dimensions[dimension] for x in self._points]
Функция _dimension_slice() - это удобный метод, который можно представить как метод, возвращающий столбец данных. Он возвращает список, состоящий из всех значений для определенного индекса каждой единицы данных. Например, если бы единицы данных имели тип DataPoint, то _dimension_slice(0) вернул бы список значений первого измерения каждой единицы данных. Это будет полезно в следующем методе нормализации:
def _zscore_normalize(self) -> None:
zscored: List[List[float]] = [[] for _ in range(len(self._points))]
for dimension in range(self._points[0].num_dimensions):
dimension_slice: List[float] = self._dimension_slice(dimension)
for index, zscore in enumerate(zscores(dimension_slice)):
zscored[index].append(zscore)
for i in range(len(self._points)):
self._points[i].dimensions = tuple(zscored[i])
Функция _zscore_normalize() заменяет значения в кортеже измерений каждой единицы данных эквивалентом ее z-оценки. При этом используется функция zscores(), которую мы определили ранее для последовательностей данных типа float. Значения в кортеже dimensions заменены, но кортеж _originals в DataPoint не изменился. Это полезно: если значения хранятся в двух местах, то после выполнения алгоритма пользователь может получить исходные значения измерений, какими они были до нормализации:
def _random_point(self) -> DataPoint:
rand_dimensions: List[float] = []
for dimension in range(self._points[0].num_dimensions):
values: List[float] = self._dimension_slice(dimension)
rand_value: float = uniform(min(values), max(values))
rand_dimensions.append(rand_value)
return DataPoint(rand_dimensions)
Описанный ранее метод _random_point() применяется в методе __init__() для создания начальных случайных центроидов для каждого кластера. Это ограничивает случайные значения каждой единицы данных в пределах диапазона значений существующих единиц данных. Метод использует конструктор, описанный ранее в DataPoint, чтобы создать новую единицу данных из итерируемого объекта значений.
Теперь рассмотрим метод поиска подходящего кластера для единицы данных:
# Найти ближайший центроид кластера для каждой единицы данных
# и назначить единицу данных этому кластеру
def _assign_clusters(self) -> None:
for point in self._points:
closest: DataPoint = min(self._centroids,
key=partial(DataPoint.distance, point))
idx: int = self._centroids.index(closest)
cluster: KMeans.Cluster = self._clusters[idx]
cluster.points.append(point)
Мы уже создали несколько функций, которые находят минимум или максимум в заданном списке. Эта функция того же рода. В данном случае мы ищем кластерный центроид с минимальным расстоянием до каждой отдельной единицы данных. Затем эта единица данных присваивается кластеру. Единственным сложным моментом является то, что при использовании функции, опосредованной partial(), в качестве key для min(). partial() принимается функция и перед применением ей задаются некоторые параметры. В данном случае мы предоставляем методу DataPoint.distance() в качестве параметра other единицу данных, которую вычисляем. Это приведет к тому, что функция min() будет возвращать расстояние каждого центроида до вычисляемой единицы данных и минимальное расстояние до центроида:
# Найти центр каждого кластера и переместить центроид туда
def _generate_centroids(self) -> None:
for cluster in self._clusters:
if len(cluster.points) == 0:
# оставить тот же центроид, если нет точек
continue
means: List[float] = []
for dimension in range(cluster.points[0].num_dimensions):
dimension_slice: List[float] = \
[p.dimensions[dimension] for p in cluster.points]
means.append(mean(dimension_slice))
cluster.centroid = DataPoint(means)
После того как все единицы данных назначены кластерам, вычисляются новые центроиды. Сюда входит вычисление среднего для каждого измерения каждой единицы данных в кластере. Затем средние значения для каждого измерения объединяются, чтобы найти среднюю точку в кластере, которая становится новым центроидом. Обратите внимание на то, что здесь нельзя использовать _dimension_ slice(), потому что рассматриваемые единицы данных являются подмножеством всех единиц данных (те, что принадлежат конкретному кластеру). Как можно переписать метод _dimension_slice(), чтобы он был более универсальным?
Теперь рассмотрим метод, который фактически выполняет алгоритм:
def run(self, max_iterations: int = 100) -> List[KMeans.Cluster]:
for iteration in range(max_iterations):
for cluster in self._clusters: # очистить все кластеры
cluster.points.clear()
self._assign_clusters()
# найти кластер, к которому текущая единица данных ближе всего
old_centroids: List[DataPoint] = deepcopy(self._centroids)
self._generate_centroids()
# записать
if old_centroids == self._centroids: # сместились ли центроиды?
print(f"Сошлось после {iteration} итерации")
return self._clusters
return self._clusters
Метод run() - наиболее чистое выражение из всего исходного алгоритма. Единственное изменение алгоритма, которое вы можете посчитать неожиданным, - это удаление всех единиц данных в начале каждой итерации. Если бы этого не произошло, метод _assign_clusters() в том виде, как он написан, в итоге поместил бы в каждый кластер дубликаты единиц данных.
Мы можем быстро протестировать алгоритм, используя тестовые объекты DataPoint и присвоив k значение 2:
if __name__ == "__main__": point1: DataPoint = DataPoint([2.0, 1.0, 1.0]) point2: DataPoint = DataPoint([2.0, 2.0, 5.0]) point3: DataPoint = DataPoint([3.0, 1.5, 2.5]) kmeans_test: KMeans[DataPoint] = KMeans(2, [point1, point2, point3]) test_clusters: List[KMeans.Cluster] = kmeans_test.run() for index, cluster in enumerate(test_clusters): print(f"Кластер {index}: {cluster.points}")
Из-за элемента случайности наши результаты могут различаться. Должно получиться что-то вроде следующего:
Сошлось после 1 итерации Кластер 0: [(2.0, 2.0, 5.0)] Кластер 1: [(2.0, 1.0, 1.0), (3.0, 1.5, 2.5)]
На следующем шаге мы рассмотрим пример его использования.
