На этом шаге мы рассмотрим общий принцип обратного распространения.
Последняя и самая сложная часть головоломки - это обратное распространение. Обратное распространение позволяет обнаружить ошибку в выходных данных нейронной сети и задействовать ее для изменения весов нейронов. Сильнее всего изменяются нейроны, больше других ответственные за ошибку. Но откуда берется ошибка? Как ее распознать? Ошибки возникают на этапе использования нейронной сети, называемом обучением.
Здесь обычным языком описаны этапы, которые можно представить несколькими математическими формулами. На рисунках приводятся псевдоформулы (без принятых в математике обозначений).
Благодаря такому подходу формулы становятся удобочитаемыми для тех, кто не связан с математикой или не использует математические обозначения. Если вас интересуют более формальная запись
и вывод формул, ознакомьтесь с главой 18 книги "Искусственный интеллект" Рассела и Норвига.
Прежде чем с нейронной сетью можно будет работать, ее, как правило, необходимо обучить. Но мы должны знать правильные выходные данные для определенных входных данных, чтобы можно было, используя разницу между ожидаемыми и фактическими выходными данными, находить ошибки и изменять веса. Другими словами, нейронные сети ничего не знают, пока им не сообщат правильные ответы для определенного набора входных данных, чтобы потом они могли подготовиться к другим входным данным. Обратное распространение происходит только во время обучения.
Поскольку большинство нейронных сетей нуждается в обучении, их относят к типу контролируемого машинного обучения. Напомним: как было показано в предыдущих шагах, алгоритм k-средних
и другие кластерные алгоритмы считаются формой неконтролируемого машинного обучения, поскольку после их запуска внешнее вмешательство не требуется. Существуют и другие типы нейронных
сетей, отличные от описанных здесь, которые не требуют предварительной подготовки и считаются формой неконтролируемого обучения.
Первым шагом при обратном распространении является вычисление ошибки между выходным сигналом нейронной сети для некоторого входного сигнала и ожидаемым выходным сигналом. Эта ошибка распространяется на все нейроны в выходном слое. (Для каждого нейрона есть ожидаемый и фактический выходной сигнал.) Затем к тому, что было бы выходным сигналом нейрона до того, как была задействована его функция активации, применяется производная функции активации выходного нейрона. (Мы кэшируем результат его функции перед активацией.) Этот результат умножают на ошибку нейрона, чтобы найти его дельту. Формула вычисления дельты использует частную производную (нахождение этой производной выходит за рамки нашего изложения). Главное, что мы получаем в результате, - то, за какое количество ошибок отвечает каждый выходной нейрон. Диаграмма вычисления показана на рисунке 1.
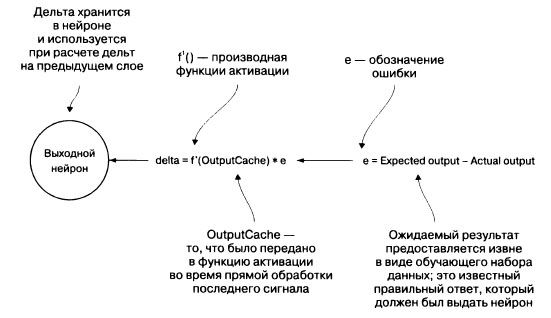
Рис.1. Механизм, с помощью которого вычисляется дельта выходного нейрона на этапе обучения посредством обратного распространения
Затем необходимо вычислить дельты для всех нейронов скрытого слоя (слоев) данной сети. Нужно определить, насколько каждый нейрон ответственен за неправильный выходной сигнал в выходном слое. Дельты выходного слоя используются для вычисления дельт в предыдущем скрытом слое. Для каждого предыдущего слоя дельты вычисляются определением скалярного произведения весов следующего слоя по отношению к конкретному рассматриваемому нейрону и уже вычисленных дельт в следующем слое. Чтобы получить дельту нейрона, это значение умножается на производную от функции активации, применяемой к последнему выходному сигналу нейрона, кэшированному перед задействованием функции активации. Эта формула также получена с помощью частной производной, подробнее о которой вы можете прочитать в более специализированных математических текстах.
На рисунке 2 показан фактический расчет дельт для нейронов в скрытых слоях.
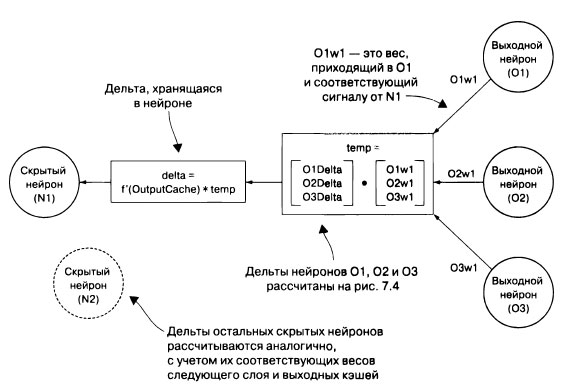
Рис.2. Вычисление дельты для нейрона в скрытом слое
В сети с несколькими скрытыми слоями нейроны O1, O2 и O3 могут быть нейронами следующего скрытого слоя, а не нейронами выходного слоя.
И последнее, но самое главное: все веса для каждого нейрона в сети должны быть обновлены путем умножения последнего входного значения каждого отдельного веса на дельту нейрона и нечто, называемое скоростью обучения, и прибавления этого значения к существующему весу. Этот метод изменения веса нейрона называется градиентным спуском. Он похож на спуск с холма, где холм - это график функции ошибки нейрона, к точке минимальной ошибки. Дельта - это направление, в котором мы хотим спускаться, а скорость обучения определяет то, как быстро будем это делать. Трудно определить хорошую скорость обучения для неизвестной задачи без проб и ошибок. На рисунке 3 показано, как изменяются веса в скрытом и выходном слоях.
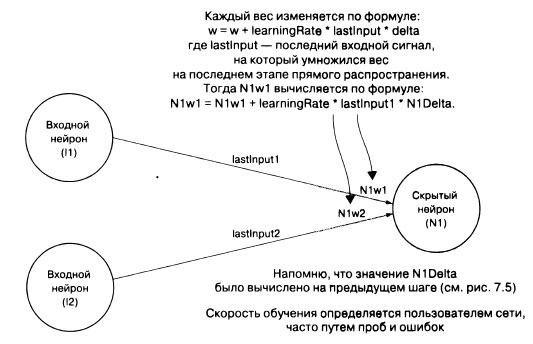
Рис.3. Веса каждого скрытого слоя и нейрона выходного слоя обновляются с использованием дельт, рассчитанных на предыдущих шагах, предыдущих весов, предыдущих входных данных и заданной пользователем скорости обучения
После изменения весов нейронная сеть готова к повторному обучению с другим набором входных и ожидаемых выходных данных. Процесс повторяется до тех пор, пока пользователь нейронной сети не сочтет, что сеть хорошо обучена. Это можно определить, проверив сеть по входным данным с известными правильными выходными данными.
Обратное распространение - сложный процесс. Не беспокойтесь, если вы еще не поняли все его детали. Объяснения, представленного в этом разделе, может оказаться недостаточно. В идеале реализация обратного распространения выведет ваше понимание на новый уровень. При реализации нашей нейронной сети и обратного распространения помните главное: обратное распространение - это способ корректировки каждого отдельного веса в сети в соответствии с тем, насколько верно он определяет неправильные выходные данные.
На следующем шаге мы рассмотрим ситуацию в целом.
