На этом шаге мы рассмотрим особенности использования этой функции.
Напомним, что функция активации преобразует выходные данные нейрона перед тем, как сигнал перейдет на следующий слой. Функция активации имеет две цели:
- она позволяет нейронной сети представлять решения, которые не являются всего лишь линейными преобразованиями (если сама функция активации является чем-то большим, нежели линейное преобразование), и
- может делать так, чтобы выходные данные каждого нейрона не выходили за пределы заданного диапазона.
Функция активации должна иметь вычислимую производную, чтобы ее можно было использовать для обратного распространения.
Популярным множеством функций активации являются сигмоидные функции. Одна из самых широко распространенных сигмоидных функций, часто называемая просто сигмоидной функцией, показана на рисунке 1 (обозначена S(x)).
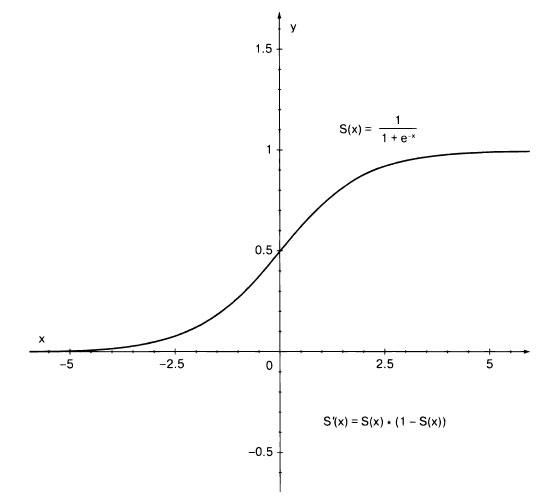
Рис.1. Сигмоидная функция активации S(x) всегда возвращает значение в диапазоне 0...1. Обратите внимание на то, что ее производную S'(x) также легко вычислить
Там же приводятся ее уравнение и производная S'(x). Результатом сигмоидной функции всегда будет значение в диапазоне 0...1. Как мы вскоре узнаем, то, что это число всегда находится в пределах от 0 до 1, полезно для сети. В тексте ниже формулы, показанные на этом рисунке, реализованы в виде кода.
Существуют и другие функции активации, но мы будем использовать сигмоидную функцию. Вот прямое преобразование формул, показанных на рисунке 1, в код (файл util.py).
# классическая сигмоидная функция активации def sigmoid(x: float) -> float: return 1.0 / (1.0 + exp(-x)) def derivative_sigmoid(x: float) -> float: sig: float = sigmoid(x) return sig * (1 - sig)
Со следующего шага мы начнем заниматься построением сети.
