На этом шаге мы рассмотрим, что это такое.
Минимакс - это классический алгоритм для поиска наилучшего хода в игре с двумя игроками, нулевой суммой и отличной информацией, такой как крестики-нолики, шашки или шахматы. Этот алгоритм был расширен и модифицирован для других типов игр. Минимакс обычно реализуется с использованием рекурсивной функции, в которой каждый игрок обозначается как максимизирующий или минимизирующий.
Максимизирующий игрок стремится найти ход, который приведет к максимальному выигрышу. Однако максимизирующий игрок должен учитывать ходы минимизирующего игрока. После каждой попытки максимизирующего игрока максимизировать выигрыш рекурсивно вызывается минимакс, чтобы найти ответ противника, который минимизирует максимизирующий выигрыш игрока. Это продолжается в обоих направлениях (максимизация, минимизация, максимизация и г. д.), пока не будет достигнут базовый случай рекурсивной функции. Базовый случай - это конечная позиция (выигрыш или ничья) либо достижение максимальной глубины поиска.
Минимакс вычисляет стартовую позицию для максимизирующего игрока. Для метода evaluate() класса TTTBoard, если наилучшая возможная игра обеих сторон приведет к выигрышу максимизирующего игрока, возвращается 1 балл.
Если наилучшая возможная игра приведет к проигрышу, то возвращается -1. Наконец, если наилучшая игра - это ничья, то возвращается 0.
Эти числа возвращаются при достижении базового случая. Затем они передаются через все рекурсивные вызовы, которые привели к базовому случаю. Чтобы максимизировать каждый рекурсивный вызов, вверх по рекурсии передаются наилучшие вычисленные ходы. Чтобы минимизировать каждый рекурсивный вызов, передаются худшие вычисленные ходы. Таким образом строится дерево решений. На рисунке 1 показано такое дерево, которое упрощает передачу данных вверх по рекурсивным вызовам для игры, в которой осталось сделать два хода.
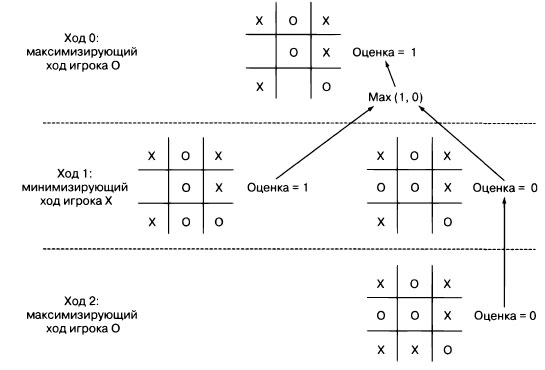
Рис.1. Минимаксное дерево решений для игры в крестики-нолики, в которой осталось сделать два хода. Чтобы максимизировать вероятность выигрыша, первоначальный
игрок, 0, должен поставить 0 по центру в нижнем ряду. Стрелки указывают позиции, с которых принимается решение
Для игр, имеющих слишком глубокое пространство поиска, таких как шашки и шахматы, чтобы достичь конечной позиции, минимакс останавливается после достижения определенной глубины (выполнения заданного количества ходов поиска, иногда называемого ply). Затем включается функция оценки, использующая эвристику для оценки состояния игры. Чем лучше выглядит игра для первого игрока, тем выше присуждаемая ей оценка. Мы вернемся к этой концепции, когда будем обсуждать игру Connect Four, которая имеет гораздо большее пространство поиска, чем крестики-нолики.
Ниже представлена полная реализация функции minimax() (файл minimax.py).
from __future__ import annotations from board import Piece, Board, Move # Находим наилучший из возможных результатов для первого игрока def minimax(board: Board, maximizing: bool, original_player: Piece, max_depth: int = 8) -> float: # Базовый случай - достигнута финальная позиция # или максимальная глубина поиска if board.is_win or board.is_draw or max_depth == 0: return board.evaluate(original_player) # Рекурсивный случай - максимизируйте свою выгоду # или минимизируйте выгоду противника if maximizing: best_eval: float = float ("-inf") # произвольно низкая начальная точка for move in board.legal_moves: result: float = minimax(board.move(move), False, original_player, max_depth - 1) best_eval = max(result, best_eval) # ищем переход с самой высокой оценкой return best_eval else: # минимизация worst_eval: float = float("inf") for move in board.legal_moves: result = minimax(board.move(move), True, original_player, max_depth - 1) worst_eval = min(result, worst_eval) # ищем переход с самой низкой оценкой return worst_eval
При каждом рекурсивном вызове нужно отслеживать позицию на поле независимо от того, максимизируем мы ее или минимизируем и для кого пытаемся оценить позицию (original_player). Первые несколько строк функции minimax() касаются базового случая - заключительной позиции (выигрыш, проигрыш или ничья) или максимально достижимой глубины. Остальная часть функции обрабатывает рекурсивные случаи.
Один из рекурсивных случаев - это максимизация. В этой ситуации мы ищем ход, который даст максимально возможную оценку. Второй рекурсивный случай - минимизация: ищем ход, который приведет к наименьшей возможной оценке. Как бы то ни было, эти два случая чередуются, пока не будет достигнута финальная позиция или максимальная глубина поиска (базовый случай).
К сожалению, мы не можем использовать нашу реализацию minimax(), чтобы найти наилучший ход для данной позиции, так как функция возвращает оценку - значение с плавающей запятой. Оно не сообщает, какой лучший первый ход привел к данной оценке.
Вместо этого создадим вспомогательную функцию find_best_move(), которая перебирает вызовы minimax() для каждого допустимого хода из данной позиции и позволяет найти ход, который имел бы максимальную оценку. Функцию find_best_move() можно представить как первый максимизирующий вызов minimax(), но с отслеживанием начальных ходов (файл minimax.py).
# Найти наилучший возможный ход из текущей позиции, # просматривая max_depth ходов вперед def find_best_move(board: Board, max_depth: int = 8) -> Move: best_eval: float = float("-inf") best_move: Move = Move(-1) for move in board.legal_moves: result: float = minimax(board.move(move), False, board.turn, max_depth) if result > best_eval: best_eval = result best_move = move return best_move
Теперь у нас есть все необходимое, чтобы найти наилучший возможный ход для любой позиции при игре в крестики-нолики.
На следующем шаге мы рассмотрим тестирование минимакса для игры в крестики-нолики.
