На этом шаге мы рассмотрим задачу о заполнении рюкзака.
Это задача оптимизации, которая касается типичной потребности, часто возникающей при вычислениях, - найти наилучший вариант использования ограниченных ресурсов при ограниченном наборе вариантов - и превращает ее в забавную историю. Вор входит в дом с намерением обчистить его. У него есть рюкзак, и он может вынести из дома только то, что туда поместится. Как узнать, что стоит положить в рюкзак? Задача проиллюстрирована на рисунке 1.
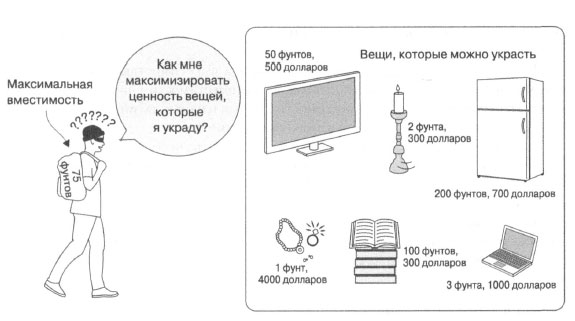
Рис.1. Взломщику необходимо решить, какие предметы украсть, потому что вместимость рюкзака ограничена
Если бы вор имел возможность взять любое количество какой-либо вещи, то он мог бы просто разделить ценность каждого предмета на его вес, чтобы определить наиболее ценные из них, способные поместиться в доступную емкость. Но мы сделаем сценарий более реалистичным: допустим, вор не может взять часть предмета, например 2,5 телевизора. Вместо этого придумаем способ решения задачи в так называемом формате 0/1, в котором применяется другое правило: вор может или взять предмет целиком, или же не брать его вовсе.
Прежде всего определим кортеж NamedTuple для хранения вещей.
from typing import NamedTuple, List class Item(NamedTuple): name: str weight: int value: float
Если бы мы попытались решить эту задачу методом грубой силы, нам пришлось бы рассмотреть каждую комбинацию предметов, которые можно положить в рюкзак. Те, у кого есть склонности к математике, называют это множеством всех подмножеств, и множество всех подмножеств для данного множества (в нашем случае множества предметов) состоит из 2N возможных подмножеств, где N - количество предметов. Поэтому нам необходимо проанализировать 2N комбинаций (O(2N)). Для небольшого количества предметов это нормально, но для большого - не годится. Следует избегать любого подхода, если при нем задача решается за экспоненциальное число шагов.
Вместо этого будем использовать технологию, известную как динамическое программирование, которое по своей концепции похоже на мемоизацию (см. 4 шаг). Вместо того чтобы решать задачу методом грубой силы, при динамическом программировании решаются подзадачи, которые составляют большую задачу, их результаты сохраняются, а затем применяются для решения более крупной задачи.
Поскольку вместимость рюкзака рассматривается в отдельных шагах, задачу можно решить методом динамического программирования.
Например, чтобы решить задачу для рюкзака вместимостью 3 фунта и трех предметов, мы можем сначала решить задачу для вместимости 1 фунт и одного возможного предмета, потом для вместимости 2 фунта и одного возможного предмета и вместимости 3 фунта и одного возможного предмета.
Затем можем использовать полученные результаты, чтобы решить задачу для вместимости 1 фунт и двух возможных предметов, вместимости 2 фунта и двух возможных предметов, вместимости 3 фунта и двух возможных предметов. И наконец, решить задачу для всех трех возможных предметов.
На протяжении пути мы станем заполнять таблицу, которая будет предлагать нам наилучшее возможное решение для каждой комбинации предметов и вместимости рюкзака. Функция сначала заполнит таблицу, а затем на ее основе выберет решение.
def knapsack(items: List[Item], max_capacity: int) -> List[Item]: # построение таблицы динамического программирования table: List[List[float]] = [[0.0 for _ in range(max_capacity + 1)] for _ in range(len(items) + 1)] for i, item in enumerate(items): for capacity in range(1, max_capacity + 1): previous_items_value: float = table[i][capacity] if capacity >= item.weight: # #предмет помещается в рюкзак value_freeing_weight_for_item: float = table[i][capacity - item.weight] # только если этот предмет ценнее предыдущего table[i + 1][capacity] = max(value_freeing_weight_for_item + item.value, previous_items_value) else: # для этого предмета нет места table[i + 1][capacity] = previous_items_value # найти решение в таблице solution: List[Item] = [] capacity = max_capacity for i in range(len(items), 0, -1): # идем в обратном направлении # этот предмет уже выбран? if table[i - 1][capacity] != table[i][capacity]: solution.append(items[i - 1]) # если предмет выбран, то вычитаем его вес capacity -= items[i - 1].weight return solution
Внутренний цикл в первой части этой функции будет выполняться N * С раз, где N - количество предметов, а С - максимальная вместимость рюкзака. Следовательно, алгоритм выполняется за время O(N*С), что для большого количества предметов значительно лучше, чем метод грубой силы. Например, для 11 описанных далее предметов алгоритм грубой силы должен был бы рассмотреть 211, или 2048, комбинаций. Представленная ранее функция динамического программирования будет выполняться 825 раз, поскольку максимальная вместимость рюкзака составляет в данном случае 75 произвольных единиц (11 * 75). Эта разница будет расти экспоненциально по мере увеличения количества предметов.
Давайте посмотрим на решение в действии.
if __name__ == "__main__": items: List[Item] = [Item("телевизор", 50, 500), Item("подсвечники", 2, 300), Item("стереосистема", 35, 400), Item("ноутбук", 3, 1000), Item("еда", 15, 50), Item("одежда", 20, 800), Item("ювелирные изделия", 1, 4000), Item("книги", 100, 300), Item("принтер", 18, 30), Item("холодильник", 200, 700), Item("картина", 10, 1000)] print(knapsack(items, 75))
Если вы проверите результаты, выведенные в консоль, то увидите, что оптимальными предметами, которые можно взять, являются картина, ювелирные изденлия, одежда, ноутбук, стереосистема и подсвечники. Вот пример выходных данных, показывающий наиболее ценные для вора вещи с учетом того, что вместимость рюкзака ограниченна:
[Item(name='картина', weight=10, value=1000), Item(name='ювелирные изделия', weight=1, value=4000), Item(name='одежда', weight=20, value=800), Item(name='ноутбук', weight=3, value=1000), Item(name='стереосистема', weight=35, value=400), Item(name='подсвечники', weight=2, value=300)]
Чтобы лучше понять, как это все работает, рассмотрим некоторые особенности данной функции:
for i, item in enumerate(items):
for capacity in range(1, max_capacity + 1):
Для каждого возможного количества предметов мы перебираем в цикле все варианты вместимости рюкзака вплоть до максимальной. Обратите внимание на то, что мы говорим "каждое возможное количество предметов", а не "каждый предмет". Когда i равно 2, это означает не просто предмет номер 2, а все возможные комбинации из первых двух предметов для каждой исследуемой вместимости. item - это следующий из рассматриваемых предметов, который можно украсть:
previous_items_value: float = table[i][capacity]
if capacity >= item.weight: # #предмет помещается в рюкзак
previous_items_value - это значение последней комбинации предметов для текущей исследуемой вместимости рюкзака. Для каждой возможной комбинации предметов мы проверяем, можно ли добавить в рюкзак еще один элемент.
Если предмет весит больше, чем позволяет рассматриваемая вместимость рюкзака, то мы просто копируем значение для последней комбинации предметов, которую рассматривали для данной вместимости:
else: # для этого предмета нет места
table[i + 1][capacity] = previous_items_value
В противном случае проверяем, приведет ли добавление нового предмета к более высокой стоимости всего украденного, чем последнее сочетание предметов для той вместимости рюкзака, которую мы рассматриваем. Для этого мы прибавляем стоимость предмета к значению, уже вычисленному в таблице для предыдущей комбинации предметов. Если это значение больше, чем значение для последней комбинации предметов для текущей вместимости, то вставляем его в таблицу, если же нет - вставляем последнее значение:
value_freeing_weight_for_item: float = table[i][capacity - item.weight]
# только если этот предмет ценнее предыдущего
table[i + 1][capacity] = max(value_freeing_weight_for_item + item.value,
previous_items_value)
На этом составление таблицы завершается. Однако для того, чтобы действительно узнать, какие предметы будут в решении, нужно проделать обратную работу для максимальной вместимости и результирующей исследуемой комбинации предметов:
for i in range(len(items), 0, -1): # идем в обратном направлении
# этот предмет уже выбран?
if table[i - 1][capacity] != table[i][capacity]:
Мы начинаем с конца и перебираем таблицу справа налево, на каждом этапе проверяя, было ли изменено значение, вставленное в таблицу. Если изменено, это означает, что мы добавили новый предмет, который рассматривался в данной комбинации, потому что эта комбинация оказалась более ценной, чем предыдущая. Поэтому мы добавляем этот предмет в решение. Кроме того, по мере перемещения по таблице вместимость рюкзака уменьшается на вес предмета:
solution.append(items[i - 1])
# если предмет выбран, то вычитаем его вес
capacity -= items[i - 1].weight
И при построении таблицы, и при поиске решения вы могли заметить увеличение и уменьшение итераторов и размера таблицы на 1. Это сделано для удобства с точки зрения программирования.
Подумайте, как эта задача строится снизу вверх. В начале решения мы имеем дело с рюкзаком нулевой вместимости. Если вы подниметесь снизу вверх по таблице, то поймете, зачем нужны
дополнительные строка и столбец.
Вы все еще в замешательстве? Таблица 1 - это то, что строит функция knapsack(). Для предыдущей задачи это была бы довольно большая таблица, так что вместо этого рассмотрим таблицу для рюкзака вместимостью 3 фунта и трех предметов: спичек (1 фунт), фонарика (2 фунта) и книги (1 фунт). Предположим, что эти предметы оцениваются в 5, 10 и 15 долларов соответственно.
| Предметы | 0 фунтов | 1 фунт | 2 фунта | 3 фунта |
|---|---|---|---|---|
| Спички (1 фунт, 5 долларов) | 0 | 5 | 5 | 5 |
| Фонарик (2 фунта, 10 долларов) | 0 | 5 | 10 | 15 |
| Книга (1 фунт, 15 долларов) | 0 | 15 | 20 | 25 |
Если просматривать таблицу слева направо, то вес предметов, которые вы пытаетесь уместить в рюкзаке, увеличивается. Если просматривать таблицу сверху вниз, то количество предметов, которые вы пытаетесь поместить в рюкзак, увеличивается. В первом ряду вы пробуете поместить в рюкзак только спички. Во втором ряду выбираете наиболее ценную комбинацию из спичек и фонарика, которая может поместиться в рюкзак. В третьем ряду находите самую ценную комбинацию из всех трех предметов.
В качестве упражнения, которое поможет вам лучше понять задачу, попробуйте заполнить пустую версию этой таблицы самостоятельно, используя алгоритм, описанный в функции knapsack(), и эти же три предмета. Затем примените алгоритм, представленный в конце функции, чтобы выбрать из таблицы правильные предметы. Эта таблица соответствует переменной table в функции.
На следующем шаге мы рассмотрим задачу коммивояжера.
